题目内容
3.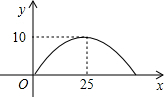 有一个抛物线形拱桥,其最大高度为10m,跨度为50m,现把它的示意图放在平面直角坐标系中,如图所示,则抛物线的函数解析式为y=-$\frac{2}{125}$(x-25)2+10.
有一个抛物线形拱桥,其最大高度为10m,跨度为50m,现把它的示意图放在平面直角坐标系中,如图所示,则抛物线的函数解析式为y=-$\frac{2}{125}$(x-25)2+10.
分析 根据题意,抛物线的顶点坐标是(25,10),并且过(0,0),利用抛物线的顶点坐标式待定系数法求它的表达式则可.
解答 解:设y=a(x-25)2+10,
因为抛物线过(0,0),
所以代入得:
625a+10=0,
即a=-$\frac{2}{125}$,
故此抛物线的函数关系式为:
y=-$\frac{2}{125}$(x-25)2+10.
故答案为:y=-$\frac{2}{125}$(x-25)2+10.
点评 本题考查了二次函数的应用,用待定系数法求函数表达式的方法,结合图象得出函数图象上点的坐标是解题关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
8.某超市以每件90元的价格购进一批商品,如果以每件100元销售,那么一个月内可售出500件,根据销售经验,销售单价每提高1元,一个月的销售量相应减少10件,如何提高售价,才能在一个月内获得最大利润?
12.下列各图中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 在一次寻宝游戏中,寻宝人已经找到了A(3,2)和B点的坐标分别为(-3,2),则宝藏的坐标(5,5)在哪里?
在一次寻宝游戏中,寻宝人已经找到了A(3,2)和B点的坐标分别为(-3,2),则宝藏的坐标(5,5)在哪里?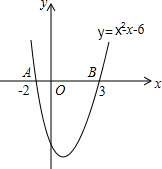 观察二次函数y=x2-x-6的图象,回答问题:
观察二次函数y=x2-x-6的图象,回答问题: