题目内容
8.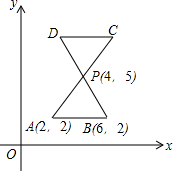 如图,AC与BD交于P点,PA=PB=PC=PD,已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5).
如图,AC与BD交于P点,PA=PB=PC=PD,已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5).(1)求出C,D的坐标;
(2)将△PAB沿AC方向平移,使P与C重合,则平移后的A,B点的坐标.
分析 (1)根据PA=PB=PC=PD,已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5),可知点C的横坐标与点A的横坐标的和的一半是点P的横坐标,点C的纵坐标与点A的纵坐标的和的一半是点P的纵坐标,同理可以求出点D的坐标;
(2)根据平移的性质,将△PAB沿AC方向平移,使P与C重合,PA=PB=PC=PD,可知平移后点A与点P重合,从而可以推出平移后点B的坐标.
解答 解:(1)设点C的坐标为(a,b),点D的坐标为(c、d).
∵PA=PB=PC=PD,△PAB的三点坐标为A(2,2),B(6,2),P(4,5),
∴$\frac{a+2}{2}=4,\frac{b+2}{2}=5$,$\frac{c+6}{2}=4,\frac{d+2}{2}=5$.
解得a=6,b=8,c=2,d=8.
∴点C的坐标为(6,8),点D的坐标是(2,8).
(2)∵将△PAB沿AC方向平移,使P与C重合,PA=PB=PC=PD,
∴平移后的A点的坐标与点P重合.
∴平移后点A的坐标为:(4,5).
∵A(2,2),B(6,2),
∴平移后点A、B的纵坐标相等,横坐标相差4.
∴平移后点B的坐标为:(10,5).
点评 本题考查坐标与图形的变化--平移,解题的关键是明白平移的性质,平移前后的对应点.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.下列方程是二元一次方程的是( )
| A. | 3x+2y=6 | B. | xy-2x-3=0 | C. | $\frac{x}{2}+\frac{5}{3}=\frac{7}{4}x$ | D. | $\frac{2}{x}+3y=2\frac{1}{3}$ |
18.-6的相反数是( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | 以上都不是 |
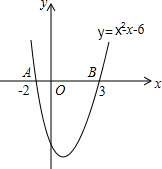 观察二次函数y=x2-x-6的图象,回答问题:
观察二次函数y=x2-x-6的图象,回答问题: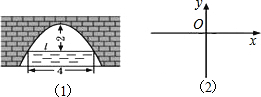 如图(1)是一个横截面为抛物线形拱桥,当拱顶高水面2m时,水面宽4m.如图(2)所示建立在平面直角坐标系中,则抛物线的解析式是y=-$\frac{1}{2}$x2.
如图(1)是一个横截面为抛物线形拱桥,当拱顶高水面2m时,水面宽4m.如图(2)所示建立在平面直角坐标系中,则抛物线的解析式是y=-$\frac{1}{2}$x2.