题目内容
5.有一个长方体纸盒,长,宽,高分别为16cm,7cm,5cm,一根长为18cm的铅笔能(填能或不能)放入这个纸盒中.分析 长方体内对角线是最长的,当木条在盒子里对角放置时,木棒长度的长度最大,所以求出盒子的对角线长度与18cm比较即可.
解答 解:如图所示: 由题意得:AC2=AB2+BC2,=162+72=305,AC′2=AC2+CC′2,
由题意得:AC2=AB2+BC2,=162+72=305,AC′2=AC2+CC′2,
故AC′2=AB2+BC2+CC′2,
从而可得对角线长度AC′=$\sqrt{A{C}^{2}+CC{′}^{2}}$=$\sqrt{305+{5}^{2}}$=$\sqrt{330}$(cm)>18cm,
∴能将一根长为18cm的铅笔放入这个盒子里面.
故答案为:能.
点评 本题考查了学生的空间想象能力及勾股定理的应用,解题的关键是熟悉勾股定理并两次应用勾股定理.

练习册系列答案
相关题目
20.下列方程是二元一次方程的是( )
| A. | 3x+2y=6 | B. | xy-2x-3=0 | C. | $\frac{x}{2}+\frac{5}{3}=\frac{7}{4}x$ | D. | $\frac{2}{x}+3y=2\frac{1}{3}$ |
14.下列方程变形正确的是( )
| A. | 由-2x=6,得x=3 | B. | 由-3=x+2,得x=-3-2 | ||
| C. | 由-7x+3=x-3,得(-7+1)x=-3-3 | D. | 由5x=2x+3,得x=-1 |
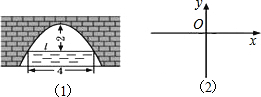 如图(1)是一个横截面为抛物线形拱桥,当拱顶高水面2m时,水面宽4m.如图(2)所示建立在平面直角坐标系中,则抛物线的解析式是y=-$\frac{1}{2}$x2.
如图(1)是一个横截面为抛物线形拱桥,当拱顶高水面2m时,水面宽4m.如图(2)所示建立在平面直角坐标系中,则抛物线的解析式是y=-$\frac{1}{2}$x2.