题目内容
16.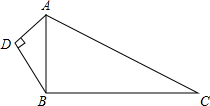 如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.
如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.
分析 由勾股定理求出AB,再求出AB2+BC2=AC2,由勾股定理的逆定理证出△ABC是直角三角形即可.
解答 解:△ABC是直角三角形;理由如下:
∵∠ADB=90°,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AB2+BC2=100+576=676=262,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
点评 本题考查了勾股定理的逆定理、勾股定理;熟练掌握勾股定理和勾股定理的逆定理,证出AB2+BC2=AC2是解决问题的关键.

练习册系列答案
相关题目
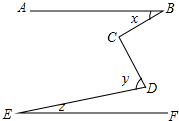 如图,已知AB∥EF,∠C=90°,求证:x+y-z=90°.
如图,已知AB∥EF,∠C=90°,求证:x+y-z=90°.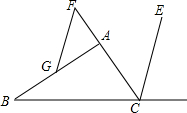 如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数.
如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数. 已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4).
已知二次函数的图象经过(0,-3),且顶点坐标为(-1,-4). 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.