题目内容
14.已知:如图1,△ABC中,AD,BE是高,AD,BE交于点F,∠ABC=45°,CD=3,AF=1,连接CF(1)判断△DCF的形状并说明理由;
(2)求AC和EF的长;
(3)如图2,有一条长度为5的线段MN在射线AD上从点A向下运动,运动过程中,当∠MNC与△BCF中的某个角度相等时,求AM的长.
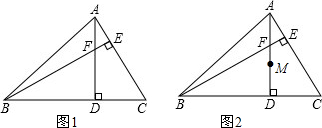
分析 (1)由AD与BE为两条高,得到一对直角相等,再由一对对顶角相等,利用内角和定理得到∠CAD=∠FBD,根据∠ABC=45°,得到三角形ABD为等腰直角三角形,即AD=BD,利用ASA得到三角形ADC与三角形BDF全等,利用全等三角形的对应边相等即可得证;
(2)由CD=3,AF=1,得到AD=BD=4,AC=5,由于S△ADC=S△DCF+S△AFC,于是得到12=9+5EF,即可得到结论;
(3)当∠MNC=∠FCB=45°,求得∠SCN=MNC=45°,得到DN=3,且MN=5,ND=2,且AD=4,求出AM=2,推出△FDB≌△CDN,根据全等三角形的性质即可得到结论.
解答 解:(1)△DCF是等腰直角三角形,
理由:∵AD、BE是△ABC的高线,
∴AD⊥BC,BE⊥AC,
∴∠ADB=∠ADC=90°,∠AEB=90°,
∵∠ABC=45°,
∴△ADB是等腰直角三角形,
∴AD=BD,
∵∠EBC+∠BFD=90°,∠CAD+∠AFE=90°,∠AFE=∠BFD,
∴∠CAD=∠EBC,
在△BDF和△ADC中,
$\left\{\begin{array}{l}{∠CAD=∠EBC}\\{AD=BD}\\{∠ADC=∠BDF=90°}\end{array}\right.$,
∴△BDF≌△ADC(ASA),
∴CD=DF,
∴△DCF是等腰直角三角形;
(2)∵CD=3,AF=1,
∴AD=BD=4,
∴AC=5,
∵S△ADC=S△DCF+S△AFC,
∴12=9+5EF,
∴EF=$\frac{3}{5}$;
(3)当∠MNC=∠FCB=45°,
∴∠SCN=MNC=45°,
∴DN=3,且MN=5,
∴ND=2,且AD=4,
∴AM=2,
当∠MNC=∠FBC,且FD=CD,∠FDC=CDN=90°,
在△FDB和△CDN中,
$\left\{\begin{array}{l}{∠MNC=∠FBC}\\{FD=CD}\\{∠FDC=∠CDN=90°}\end{array}\right.$,
∴△FDB≌△CDN,
∴BD=DN=4,且MN=5,
∴MD=1,
∴AM=3.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

 如图,在△ABC中,AB=AC,∠1=∠2,求证:∠3=∠4.
如图,在△ABC中,AB=AC,∠1=∠2,求证:∠3=∠4.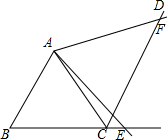 已知,如图,△ABC为等边三角形,CD∥AB,点E、F分别在BC延长线及CD上,∠EAF=60°,求证:BE=CF.
已知,如图,△ABC为等边三角形,CD∥AB,点E、F分别在BC延长线及CD上,∠EAF=60°,求证:BE=CF.
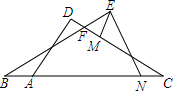 已知,如图,∠EBN+∠FCA=∠MEN,AB=CN,EN=AD.EM∥AD.探究BF与CF之间的数量关系.
已知,如图,∠EBN+∠FCA=∠MEN,AB=CN,EN=AD.EM∥AD.探究BF与CF之间的数量关系.