Question

19．如图，在△ABC中，AC=BC，在△ABC外部取一点D，连接AD、BD、CD，且CD平分∠ADB，
（1）求证：∠BCD=∠BAD；
（2）当∠ACB=60°时，将△ADB沿AB翻折点D落在点E处，连接CE，若CE⊥BE，求证：CD=3AE．

Answer 1

分析 （1）过C作CE⊥AD于E，CF⊥BD于F，根据垂直的定义得到∠CEA=∠CFB=90°，根据角平分线的性质得到CE=CF，推出Rt△ACE≌Rt△BCF，根据全等三角形的性质得到∠ACE=∠FCB，于是得到∠ACB=∠ECF，推出A，D，B，C四点共圆，根据圆周角定理即可得到结论；
（2）由已知条件得到△ACB是等边三角形，根据等边三角形的性质得到AB=BC=AC，在CD上截取CF=AD，根据全等三角形的性质得到BF=BD，由于A，C，B，D四点共圆，根据圆周角定理得到∠ECM=∠MBE，证得C，E，M，B四点共圆，于是得到BM=CE，根据折叠的性质得到AE=AD，∠ABE=∠ABD，证得∠ABE=∠ACM=∠ABD推出△ACE≌△AMB，根据全等三角形的性质得到AE=AM，证得△ADM是等边三角形，于是得到AD=DM，DF=2AD，即可得到结论．

解答 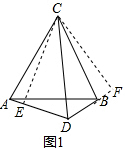解：（1）过C作CE⊥AD于E，CF⊥BD于F，
∴∠CEA=∠CFB=90°，
∵CD平分∠ADB，
∴CE=CF，
在Rt△ACE与Rt△BCF中，
$\left\{\begin{array}{l}{AC=BC}\\{CE=CF}\end{array}\right.$，
∴Rt△ACE≌Rt△BCF，
∴∠ACE=∠FCB，
∴∠ACB=∠ECF，
∵∠ECF+∠ADB=180°，
∴∠ACB+∠ADB=180°，
∴A，D，B，C四点共圆，
∴∠BCD=∠BAD；

（2）∵∠ACB=60°AC=BC，
∴△ACB是等边三角形，
∴AB=BC=AC，
在CD上截取CF=AD，
在△BCF与△ADB中，
$\left\{\begin{array}{l}{CF=AD}\\{∠DCB=∠BAD}\\{BC=AB}\end{array}\right.$，
∴△BCF≌△ADB，
∴BF=BD，
∵A，C，B，D四点共圆，
∴∠ECM=∠MBE，
∵∠BAD=∠DCB=180°-∠ADB-∠ABD=60°-∠ABD，∠EBC=∠ABC-∠ABE=60°-∠ABE，
∴∠BAD=∠EBC，
∴C，E，M，B四点共圆，
∴BM=CE，
∵将△ADB沿AB翻折点D落在点E处，
∴AE=AD，∠ABE=∠ABD，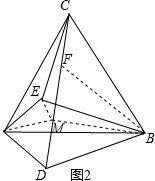
∴∠ABE=∠ACM=∠ABD，
∵∠ECM=∠EBM，
∴∠ABM=∠ACE，
在△ACE与△AMB中，
$\left\{\begin{array}{l}{AC=AB}\\{∠ABM=∠ACE}\\{BM=CE}\end{array}\right.$，
∴△ACE≌△AMB，
∴AE=AM，
∵∠ADC=60°，
∴△ADM是等边三角形，
∴AD=DM，DF=2AD．
∴CD=CF+DF=3AD．

点评 本题考查了全等三角形的判定和性质，等边三角形的性质，四点共圆，折叠的性质，正确的作出辅助线是解题的关键．