题目内容
 如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积.
如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积.考点:切线的性质,扇形面积的计算
专题:
分析:根据圆周角定理求得AC⊥BD,进而求得cos∠D=
=
=
,从而求得∠D=60°,AC=2
,根据切线的性质求得AB⊥CD,进而求得∠B=30°,进一步求得∠COA=60°,得出△OAC是等边三角形,通过解直角三角形求得AB=
=4
,即可求得OC=OA=AC=2
,从而能够求得S△AOC和S△ACD,然后根据S阴影=S△AOC+S△ACD-S扇形即可求得.
| CD |
| AD |
| 2 |
| 4 |
| 1 |
| 2 |
| 3 |
| AC |
| sin30° |
| 3 |
| 3 |
解答:解:∵AB是直径,
∴AC⊥BD,
在RT△ADC中,cos∠D=
=
=
,
∴∠D=60°,AC=2
,
∵AD切⊙O于A,AB是直径,
∴AB⊥CD,
∴∠B=30°,
∴∠COA=60°,
∵OA=OC,
∴△OAC是等边三角形,
∴AB=
=4
,
∴OC=OA=AC=2
,
∴S阴影=S△AOC+S△ACD-S扇形=
×2
×
×2
+
×2×2
-
=5
-2π.
∴AC⊥BD,
在RT△ADC中,cos∠D=
| CD |
| AD |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠D=60°,AC=2
| 3 |
∵AD切⊙O于A,AB是直径,
∴AB⊥CD,
∴∠B=30°,
∴∠COA=60°,
∵OA=OC,
∴△OAC是等边三角形,
∴AB=
| AC |
| sin30° |
| 3 |
∴OC=OA=AC=2
| 3 |
∴S阴影=S△AOC+S△ACD-S扇形=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
60π×(2
| ||
| 360 |
| 3 |
点评:本题考查了圆周角定理,切线的性质,扇形面积的计算以及等边三角形的判定等,熟练掌握性质定理是解题的关键.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
在实数范围内
有意义,则x的取值范围是( )
| x-2 |
| A、x>2 | B、x≤0 |
| C、x≥2 | D、x<0 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.
如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.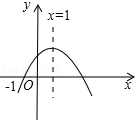 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0,②4a-2b+c<0,③ac>0,④当-1<x<3时,y>0,⑤当x≥1时,y随x的增大而增大,正确结论的序号是
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0,②4a-2b+c<0,③ac>0,④当-1<x<3时,y>0,⑤当x≥1时,y随x的增大而增大,正确结论的序号是 市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.