题目内容
9.生活中的数学:
(1)如图1所示,一扇窗户打开后,用窗钩AB要将其固定,这里所运用的几何原理是:三角形的稳定性.
(2)小河的旁边有一个甲村庄(如图2所示),现计划在河岸AB上建一个泵站,向甲村供水,使得所铺设的供水管道最短,请在上图中画出铺设的管道,这里所运用的几何原理是:垂线段最短.
(3)如图3所示,在新修的小区中,有一条“Z”字形绿色长廊ABCD,其中AB∥CD,在AB,BC,CD三段绿色长廊上各修一小凉亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,只需要测出线段ME的长度(用两个字母表示线段).这样做合适吗?请说出理由.
分析 (1)根据三角形的稳定性解答;
(2)根据垂线段最短解答;
(3)首先证明△MEB≌△MFC,根据全等三角形的性质可得ME=MF.
解答 解:(1)一扇窗户打开后,用窗钩AB要将其固定,这里所运用的几何原理是三角形的稳定性;
(2)过甲向AB做垂线,运用的原理是:垂线段最短;
(3)∵AB∥CD,
∴∠B=∠C,
∵点M是BC的中点,
∴MB=MC,
在△MCF和△MBE中$\left\{\begin{array}{l}{BE=CF}\\{∠B=∠C}\\{BM=CM}\end{array}\right.$,
∴△MEB≌△MFC(SAS),
∴ME=MF,
∴想知道M与F之间的距离,只需要测出线段ME的长度.
点评 此题主要考查了垂线段的性质,三角形的稳定性,以及全等三角形的应用,关键是掌握全等三角形,对应边相等.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
19.某市5月上旬前5天的最高气温如下(单位:℃):28、29、31、29、33,对这组数据,下列说法正确的是( )
| A. | 极差是3 | B. | 极差是5 | C. | 极差是7 | D. | 极差是9 |
18.下列多项式中,在有理数范围内不能用平方差公式分解因式的是( )
| A. | -x2+y2 | B. | 4a2-(a+b)2 | C. | -a2-9b2 | D. | x2y2-1 |
 如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD.
如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD.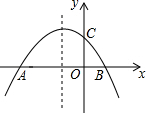 已知二次函数y=-x2-x+2的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-$\frac{1}{2}$,$\frac{3}{2}$).
已知二次函数y=-x2-x+2的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-$\frac{1}{2}$,$\frac{3}{2}$). 如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD:CD=3:2,则tanB=$\frac{\sqrt{6}}{3}$.
如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD:CD=3:2,则tanB=$\frac{\sqrt{6}}{3}$.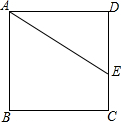 如图,在正方形ABCD中,点E在边DC上,DE=3,EC=2,把线段AE绕点A旋转后使点E落在直线BC上的点F处,则F、C两点的距离为2或8.
如图,在正方形ABCD中,点E在边DC上,DE=3,EC=2,把线段AE绕点A旋转后使点E落在直线BC上的点F处,则F、C两点的距离为2或8.