题目内容
 如图,在⊙O中,AC、BD为直径.求证:AB∥CD.
如图,在⊙O中,AC、BD为直径.求证:AB∥CD.考点:圆周角定理
专题:证明题
分析:根据圆周角定理得到∠ABC=90°,∠BCD=90°,则∠ABC+∠BCD=180°,然后根据平行线的判断即可得到结论.
解答:证明:∵AC、BD为直径,
∴∠ABC=90°,∠BCD=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
∴∠ABC=90°,∠BCD=90°,
∴∠ABC+∠BCD=180°,
∴AB∥CD.
点评:本题考查了周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
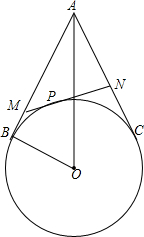 已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.
已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值. 如图所示,AB∥CD,∠A=∠F,∠D=∠E,求∠EOF的度数.
如图所示,AB∥CD,∠A=∠F,∠D=∠E,求∠EOF的度数.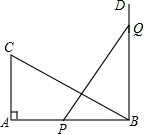 如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?
如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?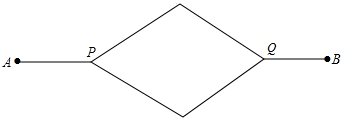 如图所示的道路,自A处出发通过P,Q到达B处,P,Q是三岔路口,假设当来到这些地点处就掷硬币,若出现正面就向右前进,若出现反面就向左前进,现若设掷硬币的次数是在四次以内,求到达B处的概率.
如图所示的道路,自A处出发通过P,Q到达B处,P,Q是三岔路口,假设当来到这些地点处就掷硬币,若出现正面就向右前进,若出现反面就向左前进,现若设掷硬币的次数是在四次以内,求到达B处的概率.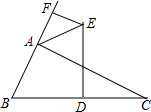 已知:△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=2,AB=3,那么AC长是
已知:△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=2,AB=3,那么AC长是