题目内容
20.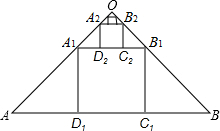 如图,在斜边长为1的等腰Rt△OAB中作内接正方形A1B1C1D1(正方形顶点都在△OAB边上),在等腰Rt△OA1B1中作内接正方形A2B2C2D2;在等腰Rt△OA2B2中,作内接正方形A3B3C3D3;…,依次作下去,则第5个正方形A5B5C5D5的边长为($\frac{1}{3}$)5.
如图,在斜边长为1的等腰Rt△OAB中作内接正方形A1B1C1D1(正方形顶点都在△OAB边上),在等腰Rt△OA1B1中作内接正方形A2B2C2D2;在等腰Rt△OA2B2中,作内接正方形A3B3C3D3;…,依次作下去,则第5个正方形A5B5C5D5的边长为($\frac{1}{3}$)5.
分析 过O作OM垂直于AB,交AB于点M,交A1B1于点N,由三角形OAB与三角形OA1B1都为等腰直角三角形,得到M为AB的中点,N为A1B1的中点,根据直角三角形斜边上的中线等于斜边的一半可得出OM为AB的一半,由AB=1求出OM的长,再由ON为A1B1的一半,即为MN的一半,可得出ON与OM的比值,求出MN的长,即为第1个正方形的边长,同理求出第2个正方形的边长,依此类推即可得到第n个正方形的边长.
解答 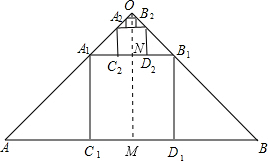 解:过O作OM⊥AB,交AB于点M,交A1B1于点N,如图所示:
解:过O作OM⊥AB,交AB于点M,交A1B1于点N,如图所示:
∵A1B1∥AB,∴ON⊥A1B1,
∵△OAB为斜边为1的等腰直角三角形,
∴OM=$\frac{1}{2}$AB=$\frac{1}{2}$,
又∵△OA1B1为等腰直角三角形,
∴ON=$\frac{1}{2}$A1B1=$\frac{1}{2}$MN,
∴ON:OM=1:3,
∴第1个正方形的边长A1C1=MN=$\frac{2}{3}$OM=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$,
同理第2个正方形的边长A2C2=$\frac{2}{3}$ON=$\frac{2}{3}$×$\frac{1}{6}$=$\frac{1}{{3}^{2}}$,
则第n个正方形AnBnDnCn的边长($\frac{1}{3}$)n.
∴第5个正方形A5B5C5D5的边长为($\frac{1}{3}$)5,
故答案为:($\frac{1}{3}$)5.
点评 此题考查了等腰直角三角形的性质,以及正方形的性质,属于一道规律型的题,熟练掌握等腰直角三角形的性质是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.下列根式中属最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{{a}^{2}}$ |
15.用反证法证明“若a⊥c,b⊥c,则a∥b”时,应假设( )
| A. | a不垂直于c | B. | a,b都不垂直于c | C. | a与b相交 | D. | a⊥b |
5.如果代数式$\frac{x-3}{\sqrt{x-2}}$有意义,那么x的取值范围是( )
| A. | x≥2 | B. | x>2且x≠3 | C. | x>2 | D. | x≥2且x≠3 |
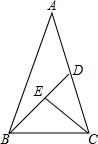 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.