题目内容
某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解析式为y=-
x2+8,BC所在抛物线的解析式为y=
(x-8)2,且已知B(m,4).
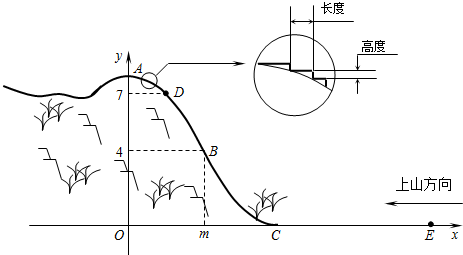
(1)设P(x,y)是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).分别求出前两级台阶的长度(精确到厘米);
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道站的起点选择在山脚水平线上的点E处,OE=1600(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为y=
(x-16)2.试求索道的最大悬空高度.
| 1 |
| 4 |
| 1 |
| 4 |

(1)设P(x,y)是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).分别求出前两级台阶的长度(精确到厘米);
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道站的起点选择在山脚水平线上的点E处,OE=1600(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为y=
| 1 |
| 28 |
考点:二次函数的应用
专题:
分析:(1)设P的坐标为(x,y)代入公式求出x与y的等式关系,然后再把B的坐标代入即可求解;
(2)利用(1)中所求得出x1的值,进而得出x2,即可得出答案;
(3)首先得出悬空高度y与x的函数关系,进而利用二次函数最值求法得出即可.
(2)利用(1)中所求得出x1的值,进而得出x2,即可得出答案;
(3)首先得出悬空高度y与x的函数关系,进而利用二次函数最值求法得出即可.
解答:解:(1)∵P(x,y)是山坡线AB上任意一点,
∴y=-
x2+8,x≥0,
∴x2=4(8-y),x=2
∵B(m,4),
∴m=2
,
∴B(4,4);
(2)在山坡线AB上,x=2
,A(0,8)
令y0=8,得x0=0;令y1=8-0.002=7.998,
得x1=2
≈0.08944,
故第一级台阶的长度为x1-x0=0.08944(百米)≈894(厘米)
同理,令y2=8-2×0.002,
可得x2≈0.12649,
故第二级台阶的长度为x2-x1=0.03705(百米)≈371(厘米);
(3)D(2,7)、E(16,0)、B(4,4)、C(8,0)由图可知,
只有当索道在BC上方时,索道的悬空高度才有可能取最大值,索道在BC上方时,
悬空高度y=
(x-16)2-
(x-8)2
=
(-3x2+40x-96)
=-
(x-
)2+
,
当x=
时,y最大=
,
故索道的最大悬空高度为
m.
∴y=-
| 1 |
| 4 |
∴x2=4(8-y),x=2
| 8-y |
∵B(m,4),
∴m=2
| 8-y |
∴B(4,4);
(2)在山坡线AB上,x=2
| 8-y |
令y0=8,得x0=0;令y1=8-0.002=7.998,
得x1=2
| 0.002 |
故第一级台阶的长度为x1-x0=0.08944(百米)≈894(厘米)
同理,令y2=8-2×0.002,
可得x2≈0.12649,
故第二级台阶的长度为x2-x1=0.03705(百米)≈371(厘米);
(3)D(2,7)、E(16,0)、B(4,4)、C(8,0)由图可知,
只有当索道在BC上方时,索道的悬空高度才有可能取最大值,索道在BC上方时,
悬空高度y=
| 1 |
| 28 |
| 1 |
| 4 |
=
| 1 |
| 14 |
=-
| 3 |
| 14 |
| 20 |
| 3 |
| 8 |
| 3 |
当x=
| 20 |
| 3 |
| 8 |
| 3 |
故索道的最大悬空高度为
| 800 |
| 3 |
点评:本题属二次函数应用中的难题.解决函数应用问题的一般步骤为:
(1)审题:弄清题意,分清条件和结论,理清数量关系;
(2)建模:将文字语言转化为数学语言,利用数学知识建立相应的数学模型;(3)求模:求解数学模型,得到数学结论;
(4)还原:将用数学方法得到的结论还原为实际问题.
(1)审题:弄清题意,分清条件和结论,理清数量关系;
(2)建模:将文字语言转化为数学语言,利用数学知识建立相应的数学模型;(3)求模:求解数学模型,得到数学结论;
(4)还原:将用数学方法得到的结论还原为实际问题.

练习册系列答案
相关题目
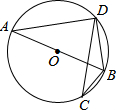 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD等于( )
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD等于( )| A、50° | B、25° |
| C、40° | D、20° |
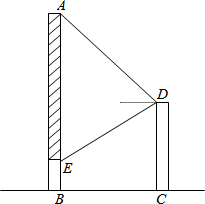 开业庆典,在甲建筑物上从A点到E点持一宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,甲乙两建筑物之间的水平距离BC为40米,这条宣传条幅AE的长(精确到0.01米).
开业庆典,在甲建筑物上从A点到E点持一宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,甲乙两建筑物之间的水平距离BC为40米,这条宣传条幅AE的长(精确到0.01米).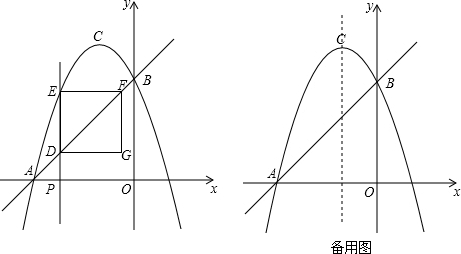
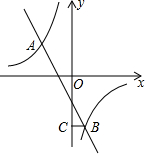 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=
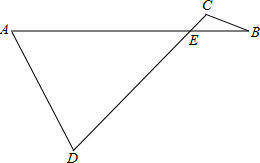 已知:AB、CD交于E点,连接AD、BC,
已知:AB、CD交于E点,连接AD、BC,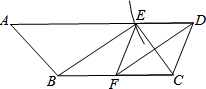 已知:如图,在梯形ABCD中,DF平分∠D,若以点D为圆心,DC长为半径作弧,交边AD于点E,联结EF、BE、EC.
已知:如图,在梯形ABCD中,DF平分∠D,若以点D为圆心,DC长为半径作弧,交边AD于点E,联结EF、BE、EC. 如图,AB∥CD,AC、BD相交于点O,BO=7,DO=3,AC=25,则AO=
如图,AB∥CD,AC、BD相交于点O,BO=7,DO=3,AC=25,则AO=