题目内容
如图，AB∥CD，AC、BD相交于点O，BO=7，DO=3，AC=25，则AO=考点：相似三角形的判定与性质
专题：
分析：由AB∥CD，可得出△OCD∽△OAB，得出比例式，代入即可求出AO的值．
解答：解：∵AB∥CD，
∠OCD=∠OAB，∠ODC=∠OBA，
∴△OCD∽△OAB，
∴
=
，
∵BO=7，DO=3，AC=25，
∴
=
，
解得AO=
，
故答案为：
．
∠OCD=∠OAB，∠ODC=∠OBA，
∴△OCD∽△OAB，
∴
| OC |
| OA |
| DO |
| BO |
∵BO=7，DO=3，AC=25，
∴
| 25-AO |
| AO |
| 3 |
| 7 |
解得AO=
| 35 |
| 2 |
故答案为：
| 35 |
| 2 |
点评：本题主要考查了相似三角形的判定与性质，解题的关键是运用三角形相似列出比例式．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
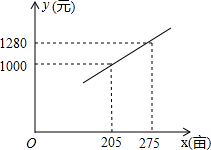国家和地方政府为了提高农民种粮的积极性，每亩地每年发放种粮补贴120元，种粮大户老王今年种了150亩地，计划明年再承租不超过90亩的土地种粮以增加收入，考虑各种因素，政府预计明年每亩种粮成本y（元）与种粮面积x（亩）之间的函数关系如图所示：