题目内容
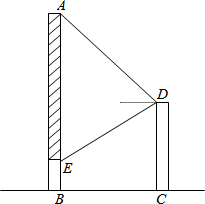开业庆典，在甲建筑物上从A点到E点持一宣传条幅（如图），在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°，测得条幅底端E点的俯角为30°，甲乙两建筑物之间的水平距离BC为40米，这条宣传条幅AE的长（精确到0.01米）．考点：解直角三角形的应用-仰角俯角问题
专题：计算题
分析：过D作DF⊥AE，交AE于点F，在直角三角形AFD中，求出AF的长，在直角三角形DFE中求出FE的长，由AF+FE即可求出AE的长．
解答：
解：过D作DF⊥AE，交AE于点F，
在Rt△ADF中，∠ADF=45°，DF=40米，
∴AF=DF=40米；
在Rt△EFD中，∠EDF=30°，DF=40米，
∴EF=DFtan30°=
米，
则AE=AF+FE=40+
≈63.09（米）．
解：过D作DF⊥AE，交AE于点F，在Rt△ADF中，∠ADF=45°，DF=40米，
∴AF=DF=40米；
在Rt△EFD中，∠EDF=30°，DF=40米，
∴EF=DFtan30°=
40
| ||
| 3 |
则AE=AF+FE=40+
40
| ||
| 3 |
点评：此题考查了解直角三角形的应用-仰角俯角问题，弄清题中的数据是解本题的关键．
练习册系列答案
相关题目
2008年我国国内生产总值（GDP）为300670亿元，用四舍五入法保留三个有效数字，用科学记数法表示为（ ）亿元．
| A、3.01×103 |
| B、3.01×105 |
| C、3.0067×105 |
| D、30.1×104 |
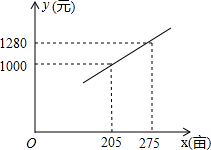国家和地方政府为了提高农民种粮的积极性，每亩地每年发放种粮补贴120元，种粮大户老王今年种了150亩地，计划明年再承租不超过90亩的土地种粮以增加收入，考虑各种因素，政府预计明年每亩种粮成本y（元）与种粮面积x（亩）之间的函数关系如图所示：