题目内容
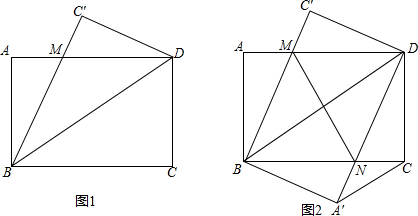
已知:如图1,在矩形ABCD中,把△BCD沿BD向上折叠,使点C落在C′处,BC′交AD于点M.
(1)求证:BM=DM;
(2)如图2,把△BAD沿BD向下折叠,使点A落在A′处,DA′交BC于点N,连接MN,判断四边形MBND是什么特殊的四边形,并说明理由;
(3)在(2)的条件下,连接MA′和MC,若CD=6,AD=8,请求出△MA′C的面积.
(1)求证:BM=DM;
(2)如图2,把△BAD沿BD向下折叠,使点A落在A′处,DA′交BC于点N,连接MN,判断四边形MBND是什么特殊的四边形,并说明理由;
(3)在(2)的条件下,连接MA′和MC,若CD=6,AD=8,请求出△MA′C的面积.

考点:矩形的性质,翻折变换(折叠问题)
专题:
分析:(1)根据矩形的性质,平行线的性质,折叠的性质和等角对等边即可证明;
(2)先证明四边形MBND是平行四边形,再根据有一组邻边相等的四边形是菱形求解即可;
(3)作A′H⊥BC于H,连接MA′,MC.先根据勾股定理得到x的值,再根据S△MA′C=S四边形MBA′C-S△MBA′列式计算即可求解.
(2)先证明四边形MBND是平行四边形,再根据有一组邻边相等的四边形是菱形求解即可;
(3)作A′H⊥BC于H,连接MA′,MC.先根据勾股定理得到x的值,再根据S△MA′C=S四边形MBA′C-S△MBA′列式计算即可求解.
解答:(1)证明:∵AD∥BC,
∴∠CBD=∠MDB,
∵∠MBD=∠CBD,
∴∠MBD=∠MDB,
∴MB=MD;
(2)菱形.理由如下
解:同理可知BN=ND,
∴∠NBD=∠NDB,
∵∠MBD=∠DBN,
∴∠MBD=∠BDN,
∴BM∥ND,
∵MD∥BN,
∴四边形MBND是平行四边形,
∵MB=MD,
∴四边形MBND是菱形;
 (3)解:作A′H⊥BC于H,连接MA′,MC,
(3)解:作A′H⊥BC于H,连接MA′,MC,
设NC=NA′=x
在RT△BA′N中BA′=6,A′N=x,BN=8-x
∴62+x2=(8-x)2,
∴x=
,
∵BA′•A′N=A′H•BN
∴A′H=
∴S△MA′C=S四边形MBA′C-S△MBA′
=
×8×6+
×8×
-
×6×
=
.
∴∠CBD=∠MDB,
∵∠MBD=∠CBD,
∴∠MBD=∠MDB,
∴MB=MD;
(2)菱形.理由如下
解:同理可知BN=ND,
∴∠NBD=∠NDB,
∵∠MBD=∠DBN,
∴∠MBD=∠BDN,
∴BM∥ND,
∵MD∥BN,
∴四边形MBND是平行四边形,
∵MB=MD,
∴四边形MBND是菱形;
 (3)解:作A′H⊥BC于H,连接MA′,MC,
(3)解:作A′H⊥BC于H,连接MA′,MC,设NC=NA′=x
在RT△BA′N中BA′=6,A′N=x,BN=8-x
∴62+x2=(8-x)2,
∴x=
| 7 |
| 4 |
∵BA′•A′N=A′H•BN
∴A′H=
| 42 |
| 25 |
∴S△MA′C=S四边形MBA′C-S△MBA′
=
| 1 |
| 2 |
| 1 |
| 2 |
| 42 |
| 25 |
| 1 |
| 2 |
| 25 |
| 4 |
=
| 2447 |
| 100 |
点评:考查了矩形的性质,翻折变换(折叠问题),涉及的知识点有:矩形的性质,平行线的性质,折叠的性质,等角对等边,平行四边形的判定,菱形的判定,勾股定理,三角形的面积计算,综合性较强,有一定的难度.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
某工厂第二季度的产值比第一季度的产值增长了x%,第三季度的产值又比第二季度的产值增长了x%,则第三季度的产值比第一季度增长了( )
| A、2x% |
| B、1+2x% |
| C、(1+x%)•x% |
| D、(2+x%)•x% |
 将方格中的帽子图形分别作以下变换:
将方格中的帽子图形分别作以下变换: