题目内容
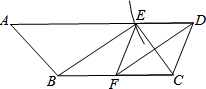 已知:如图,在梯形ABCD中,DF平分∠D,若以点D为圆心,DC长为半径作弧,交边AD于点E,联结EF、BE、EC.
已知:如图,在梯形ABCD中,DF平分∠D,若以点D为圆心,DC长为半径作弧,交边AD于点E,联结EF、BE、EC.(1)求证:四边形EDCF是菱形;
(2)若点F是BC的中点,请判断线段BE和EC的位置关系,并证明你的结论.
考点:梯形,全等三角形的判定与性质,菱形的判定与性质
专题:
分析:(1)根据圆的性质可得ED=DC,根据SAS证明△EDF≌△CDF,可得EF=CF,根据梯形的性质和平行线的性质,由等角对等边可得CF=CD,再根据菱形的判定即可求解;
(2)先根据平行四边形的判定可证四边形BEDF是平行四边形,再根据菱形的性质即可求解.
(2)先根据平行四边形的判定可证四边形BEDF是平行四边形,再根据菱形的性质即可求解.
解答:解:(1)∵DF平分∠D,
∴∠EDF=∠CDF,
∵DC长为半径作弧,
∴ED=DC,
在△EDF与△CDF中,
,
∴△EDF≌△CDF(SAS)
∴EF=CF,
∵四边形ABCD是梯形,
∴AD∥BC,
∴∠EDF=∠DFC,
∴∠DFC=∠CDF,
∴CF=CD,
∴ED=DC=CF=EF,
∴四边形EDCF是菱形.
(2)线段BE和EC的位置关系是垂直.
∵点F是BC的中点,
∴BF=CF,
∴BF=ED,
∵ED∥BF,
∴四边形BEDF是平行四边形,
∴BE∥DF
∵四边形EDCF是菱形,
∴EC⊥DF
∴BE⊥EC.
∴∠EDF=∠CDF,
∵DC长为半径作弧,
∴ED=DC,
在△EDF与△CDF中,
|
∴△EDF≌△CDF(SAS)
∴EF=CF,
∵四边形ABCD是梯形,
∴AD∥BC,
∴∠EDF=∠DFC,
∴∠DFC=∠CDF,
∴CF=CD,
∴ED=DC=CF=EF,
∴四边形EDCF是菱形.
(2)线段BE和EC的位置关系是垂直.
∵点F是BC的中点,
∴BF=CF,
∴BF=ED,
∵ED∥BF,
∴四边形BEDF是平行四边形,
∴BE∥DF
∵四边形EDCF是菱形,
∴EC⊥DF
∴BE⊥EC.
点评:考查了梯形,解决此问题,要弄清梯形的性质、全等三角形的判定与性质、平行四边形的判定和性质及菱形的判定.

练习册系列答案
相关题目
 如图:在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2厘米/秒的速度移动,点Q沿DA边从D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图:在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2厘米/秒的速度移动,点Q沿DA边从D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).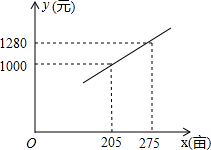 国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租不超过90亩的土地种粮以增加收入,考虑各种因素,政府预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示:
国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划明年再承租不超过90亩的土地种粮以增加收入,考虑各种因素,政府预计明年每亩种粮成本y(元)与种粮面积x(亩)之间的函数关系如图所示: