题目内容
20．小明参加班委竞选，需进行演讲答辩与民主测评，民主测评时一人一票，按“优秀、良好、一般”三选一投票，如图或表分别是五位评委对小明演讲答辩评分的条形统计图及全班50位同学民主测评票数的统计表，已知小明演讲答辩得分是95分．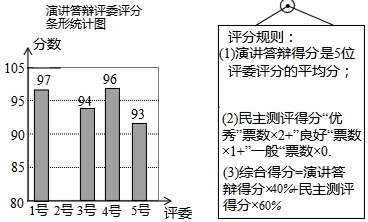
民主测评票数统计表
| 票数 | |
| 优秀 | 40 |
| 良好 | 5 |
| 一般 | 5 |
（2）根据评分规则，小明的民主测评得分是85分；
（3）求出小明的综合得分．
分析 （1）根据小明演讲答辩得分是95分，求得2号评委的分数，即可补全条形统计图；
（2）根据评分规则，即可得到小明的民主测评得分；
（3）根据评分规则，即可得到小明的综合得分．
解答 解：（1）∵小明演讲答辩得分是95分，
∴2号评委的分数为5×95-97-94-96-93=95分，
条形统计图如下：
（2）根据评分规则，小明的民主测评得分=40×2+5×1+5×0=85分，
故答案为：85；
（3）根据评分规则，小明的综合得分=95×40%+85×60%=89分．
点评 本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．解题时注意：条形统计图能清楚地表示出每个项目的数据．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
10．
下面是小东的探究学习过程，请补充完整：
（1）探究函数y=$\frac{{x}^{2}+2x-2}{2x-2}$（x＜1）的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{{x}^{2}+2x-2}{2x-2}$（x＜1）的图象与性质进行了探究．
①如表是y与x的几组对应值．
求m的值；
②如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
③进一步探究发现，该函数图象的最高点的坐标是（0，1），结合函数的图象，写出该函数的其他性质（一条即可）：当x＜0时，y随x的增大而增大；
（2）小东在（1）的基础上继续探究：他将函数y=$\frac{{x}^{2}+2x-2}{2x-2}$（x＜1）的图象向上平移1个单位长度，再向右平移1个单位长度后得到函数y=$\frac{{x}^{2}+2x-7}{2x-4}$（x＜2）的图象，请写出函数y=$\frac{{{x^2}+2x-7}}{2x-4}$（x＜2）的一条性质：函数图象的最高点坐标为（1，2）．
下面是小东的探究学习过程，请补充完整：（1）探究函数y=$\frac{{x}^{2}+2x-2}{2x-2}$（x＜1）的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{{x}^{2}+2x-2}{2x-2}$（x＜1）的图象与性质进行了探究．
①如表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{5}$ | $\frac{1}{2}$ | $\frac{4}{5}$ | … |
| y | … | -$\frac{1}{8}$ | $\frac{1}{3}$ | $\frac{3}{4}$ | $\frac{11}{12}$ | 1 | $\frac{39}{40}$ | m | -$\frac{3}{5}$ | … |
②如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
③进一步探究发现，该函数图象的最高点的坐标是（0，1），结合函数的图象，写出该函数的其他性质（一条即可）：当x＜0时，y随x的增大而增大；
（2）小东在（1）的基础上继续探究：他将函数y=$\frac{{x}^{2}+2x-2}{2x-2}$（x＜1）的图象向上平移1个单位长度，再向右平移1个单位长度后得到函数y=$\frac{{x}^{2}+2x-7}{2x-4}$（x＜2）的图象，请写出函数y=$\frac{{{x^2}+2x-7}}{2x-4}$（x＜2）的一条性质：函数图象的最高点坐标为（1，2）．
15．
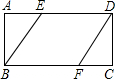如图，矩形ABCD的AB=4cm，BC=7cm，在AD、BC上分别取点E、F，四边形EBFD是菱形．那么，F到直线BE的距离是（ ）
如图，矩形ABCD的AB=4cm，BC=7cm，在AD、BC上分别取点E、F，四边形EBFD是菱形．那么，F到直线BE的距离是（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | $\sqrt{33}$cm |
12．
将一张两边平行的纸条按如图方式折叠，若∠1=100°，则∠2的度数为（ ）
将一张两边平行的纸条按如图方式折叠，若∠1=100°，则∠2的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |