题目内容
11.解下列不等式(组),并把解集在数轴上表示出来.(1)$\frac{2a-1}{3}$-4<-$\frac{a+4}{2}$
(2)$\left\{\begin{array}{l}{3a-2<a+2}\\{5a+5>2a-7}\end{array}\right.$.
分析 (1)不等式去分母,去括号,移项合并,把a系数化为1,即可求出解集;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解答 解:(1)$\frac{2a-1}{3}$-4<-$\frac{a+4}{2}$
去分母得:2(2a-1)-24<-3(a+4),
去括号得:4a-2-24<-3a-12,
移项合并得:7a<14,
解得:a<2;
把解集在数轴上表示出来为:
(2)$\left\{\begin{array}{l}{3a-2<a+2①}\\{5a+5>2a-7②}\end{array}\right.$,
由①得:a<2,
由②得:a>-4,
故不等式组的解集为-4<a<2,
把解集在数轴上表示出来为:
点评 此题考查了解一元一次不等式,解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
6.四边形ABCD中,对角线AC,BD相交于点O,且OA=OC.如果再添加一个条件使得这个四边形ABCD是平行四边形,则下列条件中不能保证满足要求的是( )
| A. | AD∥BC | B. | AD=BC | C. | AB∥CD | D. | OB=OD |
20.小明参加班委竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票,如图或表分别是五位评委对小明演讲答辩评分的条形统计图及全班50位同学民主测评票数的统计表,已知小明演讲答辩得分是95分.
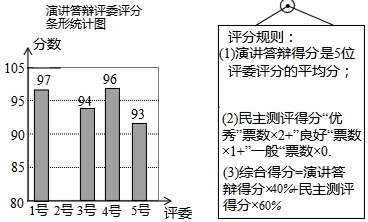
民主测评票数统计表
(1)补全条形统计图;
(2)根据评分规则,小明的民主测评得分是85分;
(3)求出小明的综合得分.

民主测评票数统计表
| 票数 | |
| 优秀 | 40 |
| 良好 | 5 |
| 一般 | 5 |
(2)根据评分规则,小明的民主测评得分是85分;
(3)求出小明的综合得分.