题目内容
6.(1)已知3m=6,3n=-2,求32m-3n-2的值;(2)利用乘法公式计算:$\frac{10{2}^{2}}{12{5}^{2}-123×127}$.
分析 (1)原式利用同底数幂的乘除法则变形,将已知等式代入计算即可求出值;
(2)原式变形后,利用平方差公式计算即可得到结果.
解答 解:(1)∵3m=6,3n=-2,
∴原式=(3m)2÷(3n)3÷9=36÷(-8)÷9=-$\frac{1}{2}$;
(2)原式=$\frac{(100+2)^{2}}{12{5}^{2}-(125-2)×(125+2)}$=$\frac{1000+400+4}{4}$=250+100+1=351.
点评 此题考查了平方差公式,同底数幂的乘除法,熟练掌握运算法则及公式是解本题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
15.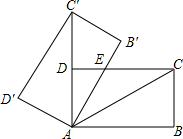 如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
 如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )| A. | 3 | B. | 1.5 | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
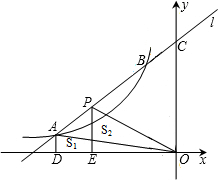 直线l交y轴于点C,与双曲线y=$\frac{k}{x}$(k<0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、P分别向x轴作垂线,垂足分别为D、E,连接OA、OP,设△AOD的面积为S1,△POE的面积为S2,则S1、S2的大小关系为S1<S2(用“<”连接).
直线l交y轴于点C,与双曲线y=$\frac{k}{x}$(k<0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、P分别向x轴作垂线,垂足分别为D、E,连接OA、OP,设△AOD的面积为S1,△POE的面积为S2,则S1、S2的大小关系为S1<S2(用“<”连接). 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)相交于A、B两点,且点A的横坐标为4.
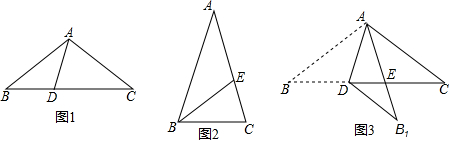
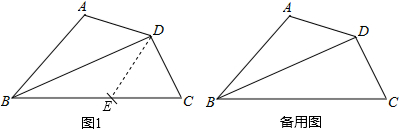
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)相交于A、B两点,且点A的横坐标为4. 在一节数学课上,老师布置了一个任务:
在一节数学课上,老师布置了一个任务: