题目内容
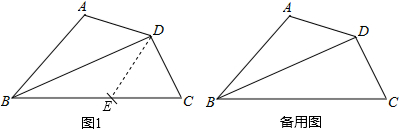
14.已知,在四边形ABCD中,对角线BD平分∠ABC,∠A+∠C=180°,求证:AD=DC.(1)如图1,小明利用圆规,添加辅助线进行证明,以点D为圆心,CD的长为半径画弧,交BC于点E,连接DE,小明的方法可行吗?请说明理由;
(2)请你用与小明不同的方法证明此题.
分析 (1)证出∠BED=∠A,由AAS证明△ABD≌△EBD,即可得出结论;
(2)作DM⊥BA于M,DN⊥BC于N,证出∠DAM=∠C,由角平分线性质得出DM=DN,由AAS证明△ADM≌△CDN,即可得出结论.
解答 (1)解:小明的方法可行;理由如下:
∵DE=CD,
∴∠DEC=∠C,
∵∠A+J5C=180°,∠BED+∠DEC=180°,
∴∠BED=∠A,
∵BD平分∠ABC,
∴∠ABD=∠EBD,
在△ABD和△EBD中,$\left\{\begin{array}{l}{∠A=∠BED}&{\;}\\{∠ABD=∠EBD}&{\;}\\{BD=BD}&{\;}\end{array}\right.$,
∴△ABD≌△EBD(AAS),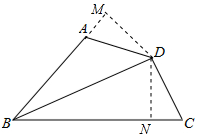
∴AD=DE,
∵DE=DC,
∴AD=DC;
(2)证明:作DM⊥BA于M,DN⊥BC于N,如图所示:
则∠DMA=∠DNC=90°,
∵∠BAD+∠C=180°,∠BAD+∠DAM=180°,
∴∠DAM=∠C,
∵BD平分∠ABC,
∴DM=DN,
在△ADM和△CDN中,$\left\{\begin{array}{l}{∠DMA=∠DNC}&{\;}\\{∠DAM=∠C}&{\;}\\{DM=DN}&{\;}\end{array}\right.$,
∴△ADM≌△CDN(AAS),
∴AD=DC.
点评 本题考查了全等三角形的判定与性质、角平分线的性质定理;熟练掌握角平分线性质定理,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
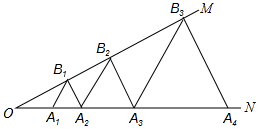 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016. 填空完成推理过程:
填空完成推理过程: 如图,?ABCD中,AE平分∠BAD,若AB=5,CE=2,则?ABCD的周长是24.
如图,?ABCD中,AE平分∠BAD,若AB=5,CE=2,则?ABCD的周长是24. 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交边AD于点E,若∠ABC=50°,求∠AEB的度数.
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交边AD于点E,若∠ABC=50°,求∠AEB的度数.