题目内容
7.判断下列命题的真假,并加以证明:(1)x2-4xy+4y2+1>1.
(2)有两条边对应相等,且相等的一条边上的中线也相等,这样的两个三角形全等.
分析 (1)当x=2y时,x2-4xy+4y2+1=1,即可判断(1)是假命题;
(2)先根据题意画出图形,再用SSS证明△ABN≌△DEM,可得到∠B=∠E,再用SAS证明△ABC≌△DEF,即可判断(2)是真命题.
解答 解:(1)∵x2-4xy+4y2+1=(x-2y)2+1,
∴当x=2y时,x-2y=0,即x2-4xy+4y2+1=1,
故(1)是假命题;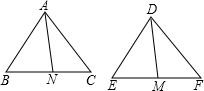 (2)已知:如图在△ABC和△DEF中,AB=DE,BC=EF,AN是BC上的中线,DM是EF上的中线,且AN=DM,
(2)已知:如图在△ABC和△DEF中,AB=DE,BC=EF,AN是BC上的中线,DM是EF上的中线,且AN=DM,
求证:△ABC≌△DEF.
证明:∵BC=EF,AN是BC上的中线,DM是EF上的中线,
∴BN=EM,
在△ABN和△DEM中,
$\left\{\begin{array}{l}{AB=DE}\\{BN=EM}\\{AN=DM}\end{array}\right.$,
∴△ABN≌△DEM(SSS),
∴∠B=∠E,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{∠B=∠E}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SAS).
点评 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.命题的“真”“假”是就命题的内容而言.任何一个命题非真即假.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.

练习册系列答案
相关题目
17.下列方程不是一元二次方程的是( )
| A. | 2x2+7=0 | B. | (x+1)(x-1)=0 | C. | 5x2+$\frac{1}{x}$+4=0 | D. | x2=1 |
18.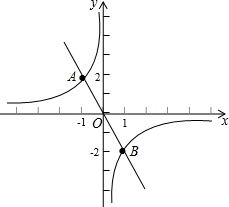 如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )
如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )
 如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )
如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )| A. | x<-1或x>1 | B. | x<-1或0<x<1 | C. | -1<x<0或 0<x<1 | D. | -1<x<0或x>1 |
19.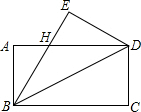 如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )
如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )
 如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )
如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )| A. | 10cm | B. | 12cm | C. | 13cm | D. | 14cm |