题目内容
分解因式：9（x+y）2-25（x-y）2．
考点：因式分解-运用公式法
专题：
分析：直接利用完全平方公式分解因式得出即可．
解答：解：9（x+y）2-25（x-y）2．
=[3（x+y）+5（x-y）][3（x+y）-5（x-y）]
=（8x-2y）（-2x+8y）
=4（4x-y）（4y-x）．
=[3（x+y）+5（x-y）][3（x+y）-5（x-y）]
=（8x-2y）（-2x+8y）
=4（4x-y）（4y-x）．
点评：此题主要考查了公式法分解因式，熟练应用平方差公式是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，E是?ABCD的一边AD上任意一点，若△EBC的面积为S1，?ABCD的面积为S，则S与S1的大小关系是（ ）A、S1=
| ||
B、S1＜
| ||
C、S1＞
| ||
| D、无法确定 |
下列四个式子中，计算结果为1012的是（ ）
| A、106+106 |
| B、（210×510）2 |
| C、（2×5×105）×106 |
| D、（103）3 |
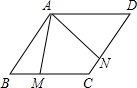如图，在?ABCD中，∠ABC=60°，AB=BC=4cm，点M，N分别在边BC，CD上，且∠MAN=60°，则四边形AMCN的面积为（ ）A、4
| ||
B、2
| ||
C、8
| ||
| D、8cm2 |
若
，则用只含x的代数式表示为（ ）
|
| A、y=2x+7 |
| B、y=7-2x |
| C、y=-2x-5 |
| D、y=2x-5 |
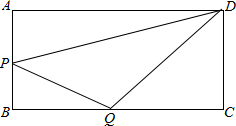在矩形ABCD中，AB=5，BC=12，点P从点B开始沿AB向点A以1个单位每秒的速度移动，点Q从点B开始沿BC边向点C以2个单位每秒的速度移动，点P到点A或点Q到点C停止移动，如果P、Q分别从B同时出发，连接PQ、DQ、DP，问几秒钟时△DPQ的面积是8？