题目内容
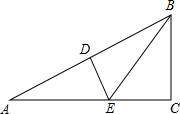 如图,△ABC中,∠C=90°,∠A=30°,作AB的垂直平分线,交AB于点D,交AC于点E,连接BE,则BE平分∠ABC.请证明这一结论.有几种证明方法呢?
如图,△ABC中,∠C=90°,∠A=30°,作AB的垂直平分线,交AB于点D,交AC于点E,连接BE,则BE平分∠ABC.请证明这一结论.有几种证明方法呢?考点:线段垂直平分线的性质,含30度角的直角三角形
专题:
分析:证明一:先根据直角三角形两锐角互余得出∠ABC=90°-∠A=60°,再由DE是AB的垂直平分线,根据线段垂直平分线的性质得出EA=EB,由等角对等边得出∠ABE=∠A=30°,于是∠EBC=∠ABC-∠ABE=30°,那么∠ABE=∠EBC,即BE平分∠ABC;
证明二:先根据30°角所对的直角边等于斜边的一半得出BC=
AB,而BD=
AB,那么BC=BD.再利用HL证明Rt△BCE≌Rt△BDE,根据全等三角形对应角相等得到∠CBE=∠DBE,即BE平分∠ABC;
证明三:先根据30°角所对的直角边等于斜边的一半得出BC=
AB,而BD=
AB,那么BC=BD.再利用勾股定理得出EC=
,ED=
,于是EC=ED,根据角平分线的判定即可证明BE平分∠ABC.
证明二:先根据30°角所对的直角边等于斜边的一半得出BC=
| 1 |
| 2 |
| 1 |
| 2 |
证明三:先根据30°角所对的直角边等于斜边的一半得出BC=
| 1 |
| 2 |
| 1 |
| 2 |
| BE2-BC2 |
| BE2-BD2 |
解答:证明一:∵△ABC中,∠C=90°,∠A=30°,
∴∠ABC=90°-∠A=60°.
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠ABE=∠A=30°,
∴∠EBC=∠ABC-∠ABE=30°,
∴∠ABE=∠EBC,
即BE平分∠ABC;
证明二:∵△ABC中,∠C=90°,∠A=30°,
∴BC=
AB,
∵BD=
AB,
∴BC=BD.
在Rt△BCE与Rt△BDE中,
,
∴Rt△BCE≌Rt△BDE(HL),
∴∠CBE=∠DBE,
即BE平分∠ABC;
证明三:∵△ABC中,∠C=90°,∠A=30°,
∴BC=
AB,
∵BD=
AB,
∴BC=BD.
∵在Rt△BCE中,由勾股定理得EC=
,
在Rt△BDE中,由勾股定理得ED=
,
∴EC=ED,
∵∠C=90°,ED⊥AB于D,
∴BE平分∠ABC.
∴∠ABC=90°-∠A=60°.
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠ABE=∠A=30°,
∴∠EBC=∠ABC-∠ABE=30°,
∴∠ABE=∠EBC,
即BE平分∠ABC;
证明二:∵△ABC中,∠C=90°,∠A=30°,
∴BC=
| 1 |
| 2 |
∵BD=
| 1 |
| 2 |
∴BC=BD.
在Rt△BCE与Rt△BDE中,
|
∴Rt△BCE≌Rt△BDE(HL),
∴∠CBE=∠DBE,
即BE平分∠ABC;
证明三:∵△ABC中,∠C=90°,∠A=30°,
∴BC=
| 1 |
| 2 |
∵BD=
| 1 |
| 2 |
∴BC=BD.
∵在Rt△BCE中,由勾股定理得EC=
| BE2-BC2 |
在Rt△BDE中,由勾股定理得ED=
| BE2-BD2 |
∴EC=ED,
∵∠C=90°,ED⊥AB于D,
∴BE平分∠ABC.
点评:本题考查了线段垂直平分线的性质,含30度角的直角三角形的性质,等腰三角形的判定,全等三角形的判定与性质,勾股定理,角平分线的判定,难度适中.

练习册系列答案
相关题目
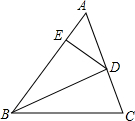 如图,在△ABC中,BD为∠ABC的平分线,DE⊥AB于点E,且DE=3cm,AB=8cm,BC=6cm,则△ABC的面积( )cm2.
如图,在△ABC中,BD为∠ABC的平分线,DE⊥AB于点E,且DE=3cm,AB=8cm,BC=6cm,则△ABC的面积( )cm2.| A、17 | B、21 | C、42 | D、52 |
 用字母表示如图所示阴影部分的面积为
用字母表示如图所示阴影部分的面积为 计算前20个“T“字形图形案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案共有多少个棋子?第2个图案与第19个图案共有多少个棋子?第3个图案第18个图案共有多少个棋子?)
计算前20个“T“字形图形案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案共有多少个棋子?第2个图案与第19个图案共有多少个棋子?第3个图案第18个图案共有多少个棋子?)