题目内容
一次函数y=kx+b的图象与x轴和y轴分别交于点A和B,已知点A和B的坐标分别为(4,0)、(0,3).
(1)求直线AB的解析式;
(2)若C是x轴上的一动点,试探究当点C运动到何处时,△CAB的面积等于△ABO面积的一半,请直接写出点C的坐标.
(1)求直线AB的解析式;
(2)若C是x轴上的一动点,试探究当点C运动到何处时,△CAB的面积等于△ABO面积的一半,请直接写出点C的坐标.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:
分析:(1)由待定系数法直接求得答案即可;
(2)设出C点的坐标,表示出△CAB的面积,与△ABO面积建立方程,求得答案即可.
(2)设出C点的坐标,表示出△CAB的面积,与△ABO面积建立方程,求得答案即可.
解答:解:(1)把(4,0)、(0,3)代入一次函数y=kx+b得,
,
解得:
.
所以函数解析式为y=-
x+3;
(2)设C点的坐标为(x,0),由题意得,
|4-x|×3=
×
×4×3,
解得:x=2或x=6.
所以点C坐标为C1(2,0),C2(6,0).
|
解得:
|
所以函数解析式为y=-
| 3 |
| 4 |
(2)设C点的坐标为(x,0),由题意得,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=2或x=6.
所以点C坐标为C1(2,0),C2(6,0).
点评:此题考查待定系数法求函数解析式,以及利用点的坐标求有关面积的问题,渗透分类探讨的思想和方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接DE,求证:
在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接DE,求证: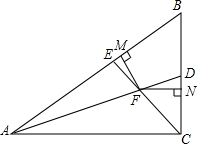 已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD. 已知,如图,AB是⊙O的直径,AC是弦,P是AC延长线上一点且AC=PC,PB的延长线交⊙O于点D.求证:AC=DC.
已知,如图,AB是⊙O的直径,AC是弦,P是AC延长线上一点且AC=PC,PB的延长线交⊙O于点D.求证:AC=DC.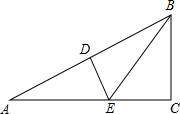 如图,△ABC中,∠C=90°,∠A=30°,作AB的垂直平分线,交AB于点D,交AC于点E,连接BE,则BE平分∠ABC.请证明这一结论.有几种证明方法呢?
如图,△ABC中,∠C=90°,∠A=30°,作AB的垂直平分线,交AB于点D,交AC于点E,连接BE,则BE平分∠ABC.请证明这一结论.有几种证明方法呢?