题目内容
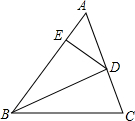 如图,在△ABC中,BD为∠ABC的平分线,DE⊥AB于点E,且DE=3cm,AB=8cm,BC=6cm,则△ABC的面积( )cm2.
如图,在△ABC中,BD为∠ABC的平分线,DE⊥AB于点E,且DE=3cm,AB=8cm,BC=6cm,则△ABC的面积( )cm2.| A、17 | B、21 | C、42 | D、52 |
考点:角平分线的性质
专题:
分析:过点D作DF⊥BC于点F,根据角平分线的性质可知DE=DF,再由S△ABC=S△ABD+S△BCD即可得出结论.
解答: 解:过点D作DF⊥BC于点F,
解:过点D作DF⊥BC于点F,
∵BD为∠ABC的平分线,DE⊥AB于点E,且DE=3cm,
∴DE=DF=3cm,
∴S△ABC=S△ABD+S△BCD=
AB•DE+
BC•DF
=
×8×3+
×6×3
=12+9
=21.
故选B.
 解:过点D作DF⊥BC于点F,
解:过点D作DF⊥BC于点F,∵BD为∠ABC的平分线,DE⊥AB于点E,且DE=3cm,
∴DE=DF=3cm,
∴S△ABC=S△ABD+S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=12+9
=21.
故选B.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
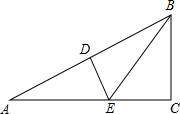 如图,△ABC中,∠C=90°,∠A=30°,作AB的垂直平分线,交AB于点D,交AC于点E,连接BE,则BE平分∠ABC.请证明这一结论.有几种证明方法呢?
如图,△ABC中,∠C=90°,∠A=30°,作AB的垂直平分线,交AB于点D,交AC于点E,连接BE,则BE平分∠ABC.请证明这一结论.有几种证明方法呢?