题目内容
3.已知2a-1的算术平方根是3,3a+b-1的平方根是±4,c是$\sqrt{13}$的整数部分,求a+2b-c的平方根.分析 先依据算术平方根和平方根的定义列出关于a、b的方程组求得a、b的值,然后估算出$\sqrt{13}$的大小,可求得c的值,接下来,求得a+2b-c的值,最后求它的平方根即可.
解答 解:由题意得:$\left\{\begin{array}{l}{2a-1=9}\\{3a+b-1=16}\end{array}\right.$,
∴a=5,b=2.
∵9<13<16,
∴3<$\sqrt{13}$<4.
∴c=3.
∴a+2b-c=6.
∴a+2b-c的平方根是±$\sqrt{6}$.
点评 本题主要考查的是算术平方根、平方根的定义、估算无理数的大小,熟练掌握相关定义和方法是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
11.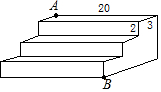 如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
 如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )| A. | 20$\sqrt{3}$ | B. | 25$\sqrt{2}$ | C. | 20 | D. | 25 |
18.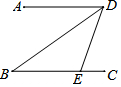 如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )
如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )
 如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )
如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )| A. | 20° | B. | 40° | C. | 60° | D. | 80° |
8.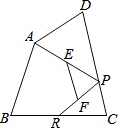 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )| A. | △EFP的周长不变 | B. | 线段EF的长与点P的位置无关 | ||
| C. | 点P到EF的距离不变 | D. | ∠APR的大小不变 |
3.点P在x轴的下方,且距离x轴3个单位长度,距离y轴4个单位长度,则点P的坐标为( )
| A. | (4,-3) | B. | (3,-4) | C. | (-3,-4)或(3,-4) | D. | (-4,-3)或(4,-3) |
4.$\frac{1}{4}$的平方根是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | ±$\frac{1}{2}$ | D. | ±$\frac{1}{16}$ |
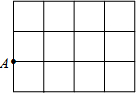 在如图所示的4×3网格中,每个小正方形的边长均为1,点A固定在格点上,请你画一个顶点都在格点上,且边长为$\sqrt{5}$的菱形ABCD,你画的菱形面积为8.
在如图所示的4×3网格中,每个小正方形的边长均为1,点A固定在格点上,请你画一个顶点都在格点上,且边长为$\sqrt{5}$的菱形ABCD,你画的菱形面积为8.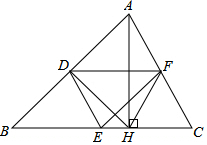 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.