题目内容
6.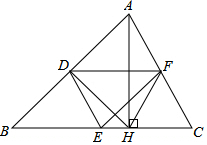 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.
分析 先根据直角三角形斜边上的中线性质得HE=$\frac{1}{2}$AC,HF=$\frac{1}{2}$AB,再判断DE和DF为△ABC的中位线得到DF=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AB,则DF=HF,DE=HF,然后根据“SSS”判断△DEF≌△FHD.
解答 证明:
∵D、E分别是AB、BC的中点
∴DE=$\frac{1}{2}$AC,
∵AH⊥BC F为AC的中点,
∴FH=$\frac{1}{2}$AC,
∴DE=FH,
同理FE=DH,
又∵DF=FD,
∴在△DEF和△FHD中
$\left\{\begin{array}{l}{DE=FH}\\{DF=FD}\\{EF=DH}\end{array}\right.$,
∴△DEF≌△FHD,
∴∠DEF=∠DHF.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.也考查了三角形中位线定理和直角三角形斜边上的中线性质.

练习册系列答案
相关题目
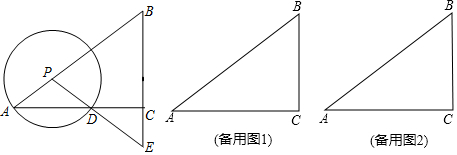
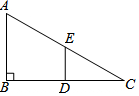 已知△ABC中,∠B=90°,D、E分别是BC、AC的中点,AB=4,BC=8,当△CDE绕点C旋转到A,E、D在同一直线上,求线段AE的长.
已知△ABC中,∠B=90°,D、E分别是BC、AC的中点,AB=4,BC=8,当△CDE绕点C旋转到A,E、D在同一直线上,求线段AE的长.