题目内容
19.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为( )| A. | 2+$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 4+2$\sqrt{3}$或2-$\sqrt{3}$ | D. | 2+$\sqrt{3}$或2-$\sqrt{3}$ |
分析 分两种情形讨论:①当圆心O在△ABC内部时.②当点O在△ABC外时.分别求解即可.
解答 解:①当圆心O在△ABC内部时,作AE⊥BC于E.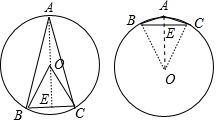
∵OB=OC,∠BOC=60°,
∴△OBC是等边三角形,
∴OB=OC=BC=2,
∴AE=OA+OE=2+$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$•BC•AE=$\frac{1}{2}$×2×(2+$\sqrt{3}$)=2+$\sqrt{3}$.
②当点O在△ABC外时,连接OA交BC于E.
S△ABC=$\frac{1}{2}$•BC•AE=$\frac{1}{2}$×2×(2-$\sqrt{3}$)=2-$\sqrt{3}$,
故选D.
点评 本题考查三角形的外接圆与外心、等腰三角形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,注意一题多解,属于中考常考题型.

练习册系列答案
相关题目
9.-$\frac{3}{4}$的倒数是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
10.若a+3=0,则a=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
4.下列计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | -$\sqrt{(-2)^{2}}$=2 | D. | $\root{3}{-8}$=-2 |
 如图,已知线段a和∠1,用直尺和圆规作等腰△ABC,使AB=AC=a,∠B=∠1(不写作法,保留作图痕迹)
如图,已知线段a和∠1,用直尺和圆规作等腰△ABC,使AB=AC=a,∠B=∠1(不写作法,保留作图痕迹)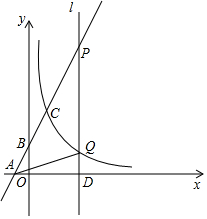 如图,在平面直角坐标系中,一次函数y=2x+2与x轴y轴分别交于点A,B与反比例函数y=$\frac{4}{x}$在第一象限交于点C.
如图,在平面直角坐标系中,一次函数y=2x+2与x轴y轴分别交于点A,B与反比例函数y=$\frac{4}{x}$在第一象限交于点C.