题目内容
15．用一个圆心角为180°，半径为4的扇形围成一个圆锥的侧面，则这个圆锥的底面圆的半径为2，该圆锥的高为2$\sqrt{3}$．分析 设这个圆锥的底面圆的半径为r，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长，利用弧长公式得到2πr=$\frac{180•π•4}{180}$，解得r=2，然后利用勾股定理计算圆锥的高．
解答 解：设这个圆锥的底面圆的半径为r，
根据题意得2πr=$\frac{180•π•4}{180}$，解得r=2，
所以圆锥的高=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$．
故答案为2，2$\sqrt{3}$．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
相关题目
如图，正方形ABCD边长为4，以BC为直径的半圆O交对角线BD于点E，则阴影部分面积为6-π．（结果保留π）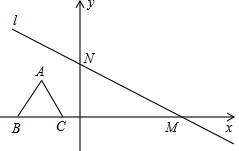
如图，在平面直角坐标系中，直线l：y=-$\frac{\sqrt{3}}{3}$x+4与x轴、y轴分别交于点M，N，高为3的等边三角形ABC，边BC在x轴上，将此三角形沿着x轴的正方向平移，在平移过程中，得到△A1B1C1，当点B1与原点重合时，解答下列问题：