题目内容
16.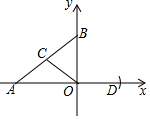 如图,在△ABO中,A(-4,0),B(0,3),OC为AB边的中线,以O为圆心,线段OC长为半径画弧,交x轴正半轴于点D,则点D的坐标为($\frac{5}{2}$,0).
如图,在△ABO中,A(-4,0),B(0,3),OC为AB边的中线,以O为圆心,线段OC长为半径画弧,交x轴正半轴于点D,则点D的坐标为($\frac{5}{2}$,0).
分析 先由勾股定理求AB=5,再根据直角三角形斜边中线等于斜边一半可得OC的长,由半径相等得OD长,从而写出D的坐标.
解答 解:∵A(-4,0),B(0,3),
∴OA=4,OB=3,
∵∠AOB=90°,
∴AB=5,
∵OC为AB边的中线,
∴OC=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴OD=OC=$\frac{5}{2}$,
∴D($\frac{5}{2}$,0);
故答案为:($\frac{5}{2}$,0).
点评 本题考查了坐标与图形的性质、直角三角形斜边中线的性质、勾股定理、圆的定义,属于基础题,明确直角三角形斜边中线等于斜边一半是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于点E,则阴影部分面积为6-π.(结果保留π)
如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于点E,则阴影部分面积为6-π.(结果保留π) 如图,一张三角形纸片ABC,∠B=45°,现将纸片的一角向内折叠,折痕ED∥BC,则∠AEB的度数为90°.
如图,一张三角形纸片ABC,∠B=45°,现将纸片的一角向内折叠,折痕ED∥BC,则∠AEB的度数为90°.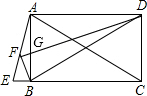 已知四边形ABCD为矩形,延长CB到E,使CE=CA,连接AE,F为AE的中点,连接BF、DF,DF交AB于点G,下列结论:
已知四边形ABCD为矩形,延长CB到E,使CE=CA,连接AE,F为AE的中点,连接BF、DF,DF交AB于点G,下列结论: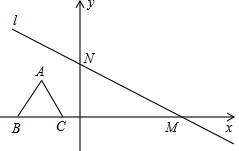 如图,在平面直角坐标系中,直线l:y=-$\frac{\sqrt{3}}{3}$x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
如图,在平面直角坐标系中,直线l:y=-$\frac{\sqrt{3}}{3}$x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题: 两个同样的直角三角板如图所示摆放,使点F,B,E,C在一条直线上,则有DF∥AC,理由是内错角相等两直线平行
两个同样的直角三角板如图所示摆放,使点F,B,E,C在一条直线上,则有DF∥AC,理由是内错角相等两直线平行