题目内容
17.关于x的多项式5x3-2mx2-2x2+3合并同类项后是三次二项式,则m满足的条件是m=-1;关于x的多项式5x3-2mx2-2x2+3合并同类项后是三次三项式,则m满足的条件是m≠-1.分析 根据合并后是三次二项式,可得二次项的系数为零,可得答案;
根据合并后是三次三项式,可得二次项的系数不为零,可得答案.
解答 解:由题意,得
-2m-2=0.解得m=-1,
由题意,得
-2m-2≠0,
解得m≠-1,
故答案为:m=-1,m≠-1.
点评 本题考查了合并同类项,利用多项式含有二次项得出关于m的方程是解题关键.

练习册系列答案
相关题目
8.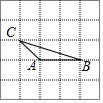 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
12.把抛物线y=$\frac{1}{2}$(x-2)2-3绕顶点旋转180°,得到的抛物线的表达式是y=-$\frac{1}{2}$(x-2)2-3,再将其向上平移3个单位,抛物线的顶点落在x轴上.
9.利用图象求得方程x2-x-1=0的近似根为( )
| A. | x1=1.6,x2=0.6 | B. | x1=-1.6,x2=0.6 | C. | x1=1.6,x2=-0.6 | D. | x1=-1.6,x2=-0.6 |
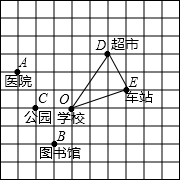 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题: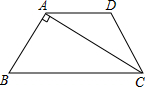 如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,tan∠DCA=$\frac{3}{4}$,AC=8,则AB的值是6.
如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,tan∠DCA=$\frac{3}{4}$,AC=8,则AB的值是6.