题目内容
12．把抛物线y=$\frac{1}{2}$（x-2）2-3绕顶点旋转180°，得到的抛物线的表达式是y=-$\frac{1}{2}$（x-2）2-3，再将其向上平移3个单位，抛物线的顶点落在x轴上．分析 根据旋转得：新抛物线的顶点不变，还是（2，-3），开口大小不变，方向相反，则a=-$\frac{1}{2}$，写出解析式，并画出图象，根据图象得：向上平移3个单位，抛物线的顶点落在x轴上．
解答 
解：把抛物线y=$\frac{1}{2}$（x-2）2-3绕顶点旋转180°，新抛物线的顶点不变，还是（2，-3），开口大小不变，方向相反，则a=-$\frac{1}{2}$，
∴得到的抛物线的表达式是：y=-$\frac{1}{2}$（x-2）2-3；
如图得，再将其向上平移3个单位，抛物线的顶点落在x轴上．
故答案为：y=-$\frac{1}{2}$（x-2）2-3，上，3．
点评 本题考查了二次函数图象与几何变换--旋转，知道旋转前后的图形大小不变，所以开口大小不变，但方向相反，即顶点不变，二次项系数a相反；利用数形结合的思想解决此题．
练习册系列答案
名校课堂系列答案
相关题目
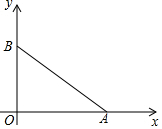如图，在平面直角坐标系xOy中，已知点（4，0），B（0，3），若有一个直角三角形与Rt△ABO全等且有一条公共的直角边，试写出这个直角三角形未知顶点的坐标．
”共504个．