题目内容
11．己知：$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$≠0，则$\frac{3x-2y-z}{z-2x-3y}$=$\frac{4}{9}$．分析 设$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$=k（k≠0），则x=2k，y=3k，z=4k，然后代入所求代数式进行计算即可．
解答 解：设$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$=k（k≠0），则x=2k，y=3k，z=4k．
原式=$\frac{6k-6k-4k}{4k-4k-9k}$=$\frac{4}{9}$．
故答案为：$\frac{4}{9}$．
点评 本题主要考查的是分式的值，用含k的式子表示出x、y、z的值是解题的关键．
练习册系列答案
相关题目
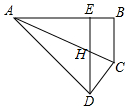如图，将Rt△ABC沿斜边AC所在直线翻折后点B落到点D，过点D作DE⊥AB，垂足为E，如果AE=3EB，EB=7，那么BC=4$\sqrt{7}$．
6．（-0.25）2003×（-4）2002的值是（ ）
| A． | -0.25 | B． | 4 | C． | -4 | D． | -2 |