题目内容
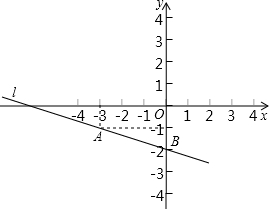 已知直线l经过A(-3,-1),B(0,-2),将该直线向上平移2个单位得到l′.
已知直线l经过A(-3,-1),B(0,-2),将该直线向上平移2个单位得到l′.(1)画出直线l′的图象;
(2)求出l′关于y轴的解析式.
考点:一次函数图象与几何变换,一次函数的图象
专题:计算题
分析:(1)先利用待定系数法求出直线l的解析式为y=-
x-2,然后根据一次函数图象与几何变换得到直线l′的解析式为y=-
x
(2)根据直线y=kx+b关于y轴对称的直线解析式为y=-kx+b进行求解.
| 1 |
| 3 |
| 1 |
| 3 |
(2)根据直线y=kx+b关于y轴对称的直线解析式为y=-kx+b进行求解.
解答:解: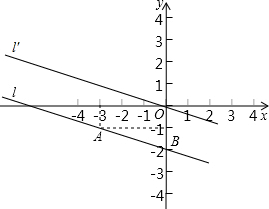 (1)设直线l的解析式为y=kx+b,
(1)设直线l的解析式为y=kx+b,
把A(-3,-1),B(0,-2)代入得
,
解得
.
所以直线l的解析式为y=-
x-2,
因为直线向上平移2个单位得到l′.
所以直线l′的解析式为y=-
x-2+2=-
x,
如图:
(2)直线l′的解析式为y=-
x关于y轴的解析式为y=
x.
 (1)设直线l的解析式为y=kx+b,
(1)设直线l的解析式为y=kx+b,把A(-3,-1),B(0,-2)代入得
|
解得
|
所以直线l的解析式为y=-
| 1 |
| 3 |
因为直线向上平移2个单位得到l′.
所以直线l′的解析式为y=-
| 1 |
| 3 |
| 1 |
| 3 |
如图:
(2)直线l′的解析式为y=-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了一次函数图象与几何变换:直线y=kx+b向上平移m(m>0)个单位所得解析式为y=kx+b+m;直线y=kx+b关于y轴对称,就是y不变,x变成-x:y=k(-x)+b,即y=-kx+b.

练习册系列答案
相关题目
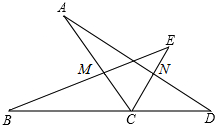 已知:如图,点B、C、D在同一条直线上,∠ACB=∠ECD=60°,AC=BC,EC=DC.连接BE、AD,分别交AC、CE于点M、N.求证:
已知:如图,点B、C、D在同一条直线上,∠ACB=∠ECD=60°,AC=BC,EC=DC.连接BE、AD,分别交AC、CE于点M、N.求证: 如图所示,用一排总长24m的篱笆一面靠墙(墙长16m)围一个长方形花圃,求花圃平行于墙的篱笆长y(m)与垂直于墙的篱笆长x(m)之间的函数解析式,求出自变量的取值范围,并画出此函数的图象.
如图所示,用一排总长24m的篱笆一面靠墙(墙长16m)围一个长方形花圃,求花圃平行于墙的篱笆长y(m)与垂直于墙的篱笆长x(m)之间的函数解析式,求出自变量的取值范围,并画出此函数的图象.