题目内容
已知a+c=b,试判断关于x的一元二次方程4ax2+4(a+b)x+a+2b+4c=0的根的情况,并说明理由.
考点:根的判别式
专题:
分析:先求出方程4ax2+4(a+b)x+a+2b+4c=0的判别式△=[4(a+b)]2-4×4a×(a+2b+4c)=16(b2-4ac),再将a+c=b代入,计算得到△=16(a-c)2,根据平方的非负性可知△≥0,由此得出方程有两个实数根.
解答:解:∵4ax2+4(a+b)x+a+2b+4c=0,
∴△=[4(a+b)]2-4×4a×(a+2b+4c)=16(b2-4ac),
∵a+c=b,
∴△=16[(a+c)2-4ac]=16(a-c)2≥0,
∴方程有两个实数根.
∴△=[4(a+b)]2-4×4a×(a+2b+4c)=16(b2-4ac),
∵a+c=b,
∴△=16[(a+c)2-4ac]=16(a-c)2≥0,
∴方程有两个实数根.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的情况与判别式△=b2-4ac的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
 已知长方体盒子的长、宽、高分别为6cm、2cm、2cm,如图所示,在顶点A处的蚂蚁要去吃顶点B处的食物,那么这只蚂蚁所要爬行的最短路线长为多少?
已知长方体盒子的长、宽、高分别为6cm、2cm、2cm,如图所示,在顶点A处的蚂蚁要去吃顶点B处的食物,那么这只蚂蚁所要爬行的最短路线长为多少?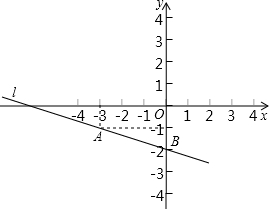 已知直线l经过A(-3,-1),B(0,-2),将该直线向上平移2个单位得到l′.
已知直线l经过A(-3,-1),B(0,-2),将该直线向上平移2个单位得到l′.