题目内容
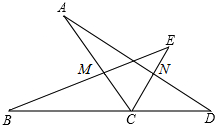 已知:如图,点B、C、D在同一条直线上,∠ACB=∠ECD=60°,AC=BC,EC=DC.连接BE、AD,分别交AC、CE于点M、N.求证:
已知:如图,点B、C、D在同一条直线上,∠ACB=∠ECD=60°,AC=BC,EC=DC.连接BE、AD,分别交AC、CE于点M、N.求证:(1)△ACD≌△BCE;
(2)CM=CN.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)由∠ACB=∠ECD根据等式的性质就可以得出∠ACD=∠BCE,再由SAS就可以得出△ACD≌△BCE;
(2)由点B、C、D在同一条直线上,就可以得出∠ACE=60°,得出△DCN≌△ECM就可以得出结论.
(2)由点B、C、D在同一条直线上,就可以得出∠ACE=60°,得出△DCN≌△ECM就可以得出结论.
解答:证明:(1)∵∠ACB=∠ECD,
∴∠ACB+∠ACE=∠ECD+∠ACE,
∴∠BCE=∠ACD.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)∵点B、C、D在同一条直线上,
∴∠BCD=180°.
∵∠ACB=∠ECD=60°,
∴∠ACE=60°,
∴∠ACE=∠DCE.
∵△ACD≌△BCE,
∴∠D=∠E.
在△DCN和△ECM中,
,
∴△DCN≌△ECM(ASA),
∴CN=CM.
∴∠ACB+∠ACE=∠ECD+∠ACE,
∴∠BCE=∠ACD.

在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS);
(2)∵点B、C、D在同一条直线上,
∴∠BCD=180°.
∵∠ACB=∠ECD=60°,
∴∠ACE=60°,
∴∠ACE=∠DCE.
∵△ACD≌△BCE,
∴∠D=∠E.
在△DCN和△ECM中,
|
∴△DCN≌△ECM(ASA),
∴CN=CM.
点评:本题考查了平角的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
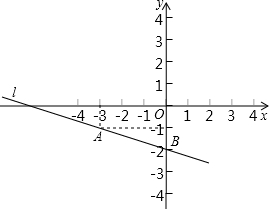 已知直线l经过A(-3,-1),B(0,-2),将该直线向上平移2个单位得到l′.
已知直线l经过A(-3,-1),B(0,-2),将该直线向上平移2个单位得到l′. 小明家的窗户如图所示,它是由一个半圆和一个长方形组成.做一个这样的窗户总材料为6m.设窗户半圆的半径为xm.怎么用关于x的代数式表示窗户的透光面积?
小明家的窗户如图所示,它是由一个半圆和一个长方形组成.做一个这样的窗户总材料为6m.设窗户半圆的半径为xm.怎么用关于x的代数式表示窗户的透光面积?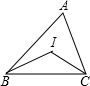 在△ABC中,BI、CI分别平分∠ABC、∠ACB,且∠A=∠α,求∠BIC的度数.
在△ABC中,BI、CI分别平分∠ABC、∠ACB,且∠A=∠α,求∠BIC的度数.