题目内容
18.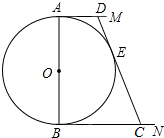 如图,⊙O的直径AB=12,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.设AD=x,BC=y,则y关于x的函数图象大致是( )
如图,⊙O的直径AB=12,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.设AD=x,BC=y,则y关于x的函数图象大致是( )| A. | 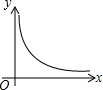 | B. |  | C. | 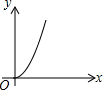 | D. | 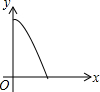 |
分析 根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系.
解答 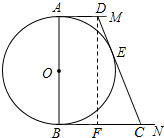 解:作DF⊥BN交BC于F;
解:作DF⊥BN交BC于F;
∵AM、BN与⊙O切于点定A、B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BC-BF=y-x;
∵DE切⊙O于E,
∴DE=DA=x CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(y-x)2+122,
整理为y=$\frac{36}{x}$,
∴y与x的函数关系式是y=$\frac{36}{x}$,
y是x的反比例函数.
故选A.
点评 此题考查了动点问题的函数图象,切线的性质、切线长定理、矩形的判定与性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
4.如图,是一石拱桥的桥拱截面示意图,已知拱桥是一段优弧,桥拱顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )


| A. | 8m | B. | 4m | C. | 6m | D. | 3m |
6.下列说法中,正确的是( )
| A. | 单项式4a+$\frac{1}{b}$m的次数是0 | |
| B. | $\frac{1}{x}$是整式 | |
| C. | -$\frac{1}{4}$不是单项式 | |
| D. | 单项式-$\frac{{{2^3}mn}}{8}$的系数是-1,次数是2 |
3.若2x2y1-2m和3xn-1y2是同类项,则mn的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |