题目内容
3.若2x2y1-2m和3xn-1y2是同类项,则mn的值是( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
分析 根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,几个常数项也是同类项.同类项与字母的顺序无关,与系数无关,进而求出即可.
解答 解:∵2x2y1-2m和3xn-1y2是同类项,
∴n-1=2,1-2m=2,
∴n=3,m=-$\frac{1}{2}$,
∴mn=-$\frac{1}{8}$,
故选D.
点评 本题考查同类项的定义,同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同;是易混点.
同类项定义中隐含的两个“无关”:①与字母的顺序无关;②与系数无关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.若(x-2)0-(x-3)-4有意义,那么x的取值范围是( )
| A. | x>2 | B. | x>3 | C. | x≠2或x≠3 | D. | x≠2且x≠3 |
13.下列运算正确的是( )
| A. | x5+x5=x10 | B. | (x3)3=x6 | C. | x3•x2=x5 | D. | x6-x3=x3 |
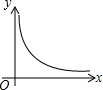
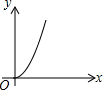
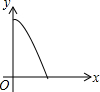
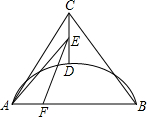 如图,AC=BC,点D是以线段AB为弦的圆弧的中点,AB=4,点E、F分别是线段CD,AB上的动点.设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是( )
如图,AC=BC,点D是以线段AB为弦的圆弧的中点,AB=4,点E、F分别是线段CD,AB上的动点.设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是( )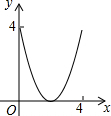
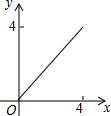
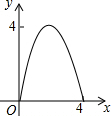
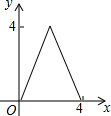
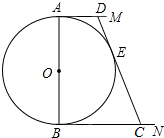 如图,⊙O的直径AB=12,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.设AD=x,BC=y,则y关于x的函数图象大致是( )
如图,⊙O的直径AB=12,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.设AD=x,BC=y,则y关于x的函数图象大致是( )