题目内容
10.(1)解方程:$\frac{x}{x+1}=\frac{2x}{3x+3}+1$.(2)先化简,再求值:1-$\frac{a-b}{a+2b}+\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$,其中a=3,b=-1.
分析 (1)先去分母,把分式方程化为整式方程,再求解即可,注意检验;
(2)先通分,再化简,最后把a=3,b=-1代入求值即可.
解答 解:(1)方程两边同乘以3(x+1)
3x=2x+3x+3
-2x=3
x=-$\frac{3}{2}$
检验:当x=-$\frac{3}{2}$时,3(x+1)≠0,
∴原方程的解为x=-$\frac{3}{2}$;
(2)原式=1-$\frac{a-b}{a+2b}$•$\frac{(a+2b)^{2}}{(a+b)(a-b)}$
=1-$\frac{a+2b}{a+b}$
=$\frac{a+b-a-2b}{a+b}$
=$\frac{-b}{a+b}$,
当a=3,b=-1时,
原式=$\frac{-b}{a+b}$=$\frac{1}{3-1}$=$\frac{1}{2}$.
点评 本题考查了分式的化简求值以及解分式方程,注意解分式方程一定要验根.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
20.现用190张铁皮制作一批盒子,每张铁皮可做8个盒身或做22个盒底,而一个盒身和两个盒底配成一个完整的盒子.问用多少张白铁皮制盒身、多少张白铁皮制盒底,可以使盒身和盒底正好配套.设用x张铁皮做盒身,y张铁皮做盒底,可以使盒身与盒底正好配套,则可列方程是( )
| A. | $\left\{\begin{array}{l}{x+2y=190}\\{8x=22y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=190}\\{2×8x=22y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+2y=190}\\{2×8x=22y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=190}\\{2×22y=8x}\end{array}\right.$ |
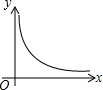
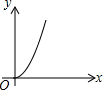
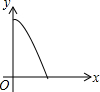
 如图,已知点P是y轴正半轴上任意一点,过点P作x轴的平行线交抛物线y=x2于点C,D(点C在点D的右边),过点C作CB⊥x轴于点B,过点D作DA⊥x轴于点A,分别以OA,OB为直径作半圆.设点P的纵坐标为h,图中阴影部分的面积为s,则s与h之间的函数关系的图象大致是( )
如图,已知点P是y轴正半轴上任意一点,过点P作x轴的平行线交抛物线y=x2于点C,D(点C在点D的右边),过点C作CB⊥x轴于点B,过点D作DA⊥x轴于点A,分别以OA,OB为直径作半圆.设点P的纵坐标为h,图中阴影部分的面积为s,则s与h之间的函数关系的图象大致是( )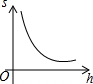



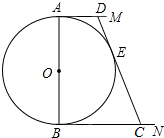 如图,⊙O的直径AB=12,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.设AD=x,BC=y,则y关于x的函数图象大致是( )
如图,⊙O的直径AB=12,AM和BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于D,C两点.设AD=x,BC=y,则y关于x的函数图象大致是( )