题目内容
 如图,添加一个条件:
如图,添加一个条件:考点:相似三角形的判定
专题:开放型
分析:根据相似三角形的判定有三种方法:
①三边法:三组对应边的比相等的两个三角形相似;
②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
③两角法:有两组角对应相等的两个三角形相似.
由此可得出可添加的条件.
①三边法:三组对应边的比相等的两个三角形相似;
②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
③两角法:有两组角对应相等的两个三角形相似.
由此可得出可添加的条件.
解答:解:由题意得,∠A=∠A(公共角),
则可添加:∠ADE=∠ACB,利用两角法可判定△ADE∽△ACB.
故答案可为:∠ADE=∠ACB(答案不唯一).
则可添加:∠ADE=∠ACB,利用两角法可判定△ADE∽△ACB.
故答案可为:∠ADE=∠ACB(答案不唯一).
点评:本题考查了相似三角形的判定,解答本题的关键是熟练掌握三角形相似的三种判定方法,本题答案不唯一.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
下列说法正确的是( )
| A、如果a+b=0,则a=b=0 | ||
| B、如果ab=0,则a=b=0 | ||
C、如果
| ||
| D、如果|a|+|b|=0,则a=b=0 |
 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=∠OAC,则∠AOC的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=∠OAC,则∠AOC的大小是( )| A、90° | B、45° |
| C、70° | D、60° |
下列说法错误的是( )
| A、-a的绝对值为a | ||
| B、-a的相反数为a | ||
C、
| ||
| D、如果|a|=-a,则a<0或a=0 |
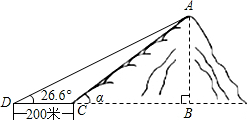 如图,小山岗的斜坡AC的坡度是
如图,小山岗的斜坡AC的坡度是 如图,△ABC的周长为30cm,DE垂直平分边AC,交BC于点D,交AC于点E,连接AD,若AE=4cm,则△ABD的周长是=
如图,△ABC的周长为30cm,DE垂直平分边AC,交BC于点D,交AC于点E,连接AD,若AE=4cm,则△ABD的周长是= 如图,在Rt△ABC中,斜边AB=13cm,直角边AC=5cm,以直线AB为轴旋转一周形成纺锤形,求这个纺锤形的表面积.
如图,在Rt△ABC中,斜边AB=13cm,直角边AC=5cm,以直线AB为轴旋转一周形成纺锤形,求这个纺锤形的表面积.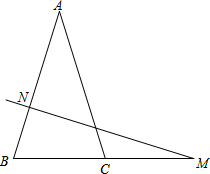 如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,
如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,