题目内容
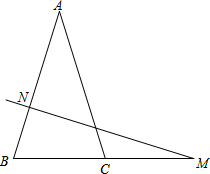 如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,
如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,(1)若∠A=30°.求∠NMB的度数;
(2)如果将(1)中∠A的度数改为68°,其余条件不变,求∠NMB的度数;
(3)综合(1)(2),你发现有什么样的规律性,试证明之;
(4)若将(1)中的∠A改为直角或钝角,你发现的规律是否仍然成立?
考点:等腰三角形的性质
专题:探究型
分析:(1)利用等腰三角形的性质可先求得∠B,在Rt△BMN中利用三角形内角和可求得∠NMB;
(2)方法同(1);
(3)利用等腰三角形的性质和三角形内角和定理可找到∠A与∠NMB之间的关系,可证明结论;
(4)结合(3)的证明,可知仍然成立,证明方法同(3).
(2)方法同(1);
(3)利用等腰三角形的性质和三角形内角和定理可找到∠A与∠NMB之间的关系,可证明结论;
(4)结合(3)的证明,可知仍然成立,证明方法同(3).
解答:解:
(1)∵AB=AC,
∴∠B=∠ACB,
∴∠B=
=90°-
∠A,
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
∠A=15°;
(2)当∠A=68°时,同理仍有∠NMB=
∠A=34°;
(3)规律:∠NMB=
∠A,证明如下:
∵AB=AC,
∴∠B=∠ACB,
∴∠B=
=90°-
∠A,
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
∠A;
(4)当∠A为钝角或直角时,仍然有∠NMB=
∠A.
(1)∵AB=AC,
∴∠B=∠ACB,
∴∠B=
| 180°-∠A |
| 2 |
| 1 |
| 2 |
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
| 1 |
| 2 |
(2)当∠A=68°时,同理仍有∠NMB=
| 1 |
| 2 |
(3)规律:∠NMB=
| 1 |
| 2 |
∵AB=AC,
∴∠B=∠ACB,
∴∠B=
| 180°-∠A |
| 2 |
| 1 |
| 2 |
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
| 1 |
| 2 |
(4)当∠A为钝角或直角时,仍然有∠NMB=
| 1 |
| 2 |
点评:本题主要考查等腰三角形的性质,掌握等边对等角及三角形内角和为180°是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
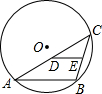 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=45°,点D、E分别是AC、BC的中点,若⊙O的半径为4,则线段DE的长为
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=45°,点D、E分别是AC、BC的中点,若⊙O的半径为4,则线段DE的长为 如图,添加一个条件:
如图,添加一个条件: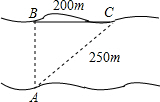 如图,小红欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了250m,则该河流的宽度为
如图,小红欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了250m,则该河流的宽度为