题目内容
如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC=∠OAC，则∠AOC的大小是（ ）| A、90° | B、45° |
| C、70° | D、60° |
考点：圆周角定理
专题：
分析：由圆周角定理可得∠AOC=2∠ABC，又由∠ABC=∠OAC，可得∠AOC=2∠OAC，然后由OA=OC，得到∠OAC=∠OCA，则可求得∠AOC的度数．
解答：解：∵∠AOC=2∠ABC，∠ABC=∠OAC，
∴∠AOC=2∠OAC，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠AOC=2∠OAC=2∠OCA，
∴∠AOC=90°．
故选A．
∴∠AOC=2∠OAC，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠AOC=2∠OAC=2∠OCA，
∴∠AOC=90°．
故选A．
点评：此题考查了圆周角定理以及等腰三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，已知△ABC≌△ADE，AD=AB，AE=AC，∠D-∠E=20°，∠BAC=60°，求∠C的度数．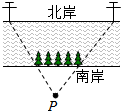
如图，一条河的两岸有一段平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆，小丽站在离南岸边15米的点P处看北岸，发现北岸相邻的两根电线恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为
如图，⊙O是△ABC的外接圆，已知∠OAB=40°，则∠ACB为
如图，添加一个条件：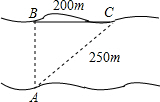
如图，小红欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B200m，结果他在水中实际游了250m，则该河流的宽度为
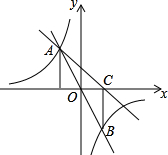如图，在平面直角坐标系xOy中，直线y=mx与双曲线y=