题目内容
1.若关于x的方程(|a|-1)x2+(a-1)x4b-3=0是一元一次方程,求代数式a2-2ab+b2的值.分析 根据二次项系数等于零且一次项系数不等于零是一元一次方程,可得a、b的值,根据完全平方公式,可得答案.
解答 解:由关于x的方程(|a|-1)x2+(a-1)x4b-3=0是一元一次方程,得
$\left\{\begin{array}{l}{|a|-1=0}\\{a-1≠0}\\{4b=1}\end{array}\right.$.
解得$\left\{\begin{array}{l}{a=-1}\\{b=\frac{1}{4}}\end{array}\right.$.
当a=-1,b=$\frac{1}{4}$时,a2-2ab+b2=(a-b)2=(-1-$\frac{1}{4}$)2=$\frac{25}{16}$.
点评 本题考查了一元一次方程的定义,二次项系数等于零且一次项系数不等于零是一元一次方程得出a、b的值是解题关键.

练习册系列答案
相关题目
 如图,小张从点B沿BO向学校O走去,此时班长接到放假通知后从点A出发沿直线去拦截小张,两人所走速度相同,且班长刚好在OB上一点P处拦到小张,请确定点P的位置.
如图,小张从点B沿BO向学校O走去,此时班长接到放假通知后从点A出发沿直线去拦截小张,两人所走速度相同,且班长刚好在OB上一点P处拦到小张,请确定点P的位置.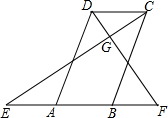 已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.
已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.