题目内容
19.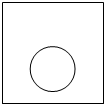 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )| A. | πr2 | B. | a2-πr2 | C. | 4r2-πr2 | D. | $\frac{a^2}{4}$ |
分析 过圆心向正方形的两边作垂线,根据圆形纸片“不能接触到的部分”的面积=4×(小正方形的面积减去四分之一圆的面积)即可得出结论.
解答  解:如图所示,过圆心向正方形的两边作垂线,
解:如图所示,过圆心向正方形的两边作垂线,
由图可知圆形纸片“不能接触到的部分”的面积=4×(小正方形的面积减去四分之一圆的面积)
=4×(r2-$\frac{1}{4}$πr2)
=4r2-πr2.
故选C.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
9.已知抛物线y=2x2-(m2+1)x+2m2-1,不论m取何值,抛物线恒过某定点P,则P点的坐标为( )
| A. | (2,-5) | B. | (2,5) | C. | (-2,5) | D. | 不能确定 |
4.下列各组数据中不能构成直角三角形的一组数据是( )
| A. | 4-$\sqrt{3}$,4+$\sqrt{3}$,$\sqrt{38}$ | B. | $\frac{5}{4}$,$\frac{3}{4}$,1 | ||
| C. | k,2k,$\sqrt{3}$k | D. | 2m2+1,2m2-1,2m(m是大于1的整数) |
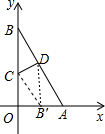 如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).
如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).