题目内容
11.已知二次函数y=x2-2x-3.(1)用配方法将解析式化为y=(x-h)2+k的形式;
(2)求这个函数图象与x轴的交点坐标.
分析 (1)利用配方法把二次函数的一般式化为顶点式即可;
(2)令y=0,得到关于x的一元二次方程,解方程即可.
解答 解:(1)y=(x2-2x+1)-4
=(x-1)2-4;
(2)令y=0,得x2-2x-3=0,
解得x1=3,x2=-1,
∴这条抛物线与x轴的交点坐标为(3,0),(-1,0).
点评 本题考查的是二次函数的三种形式以及求抛物线与x轴的交点坐标,正确利用配方法把二次函数的一般式化为顶点式是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
2.下列因式分解正确的是( )
| A. | x2-xy+x=x(x-y) | B. | x2-2x+4=(x-1)2+3 | ||
| C. | ax3-9=a(x+3)(x-3) | D. | a3-2a2b+ab2=a(a-b)2 |
3. 如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )
如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )
 如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )
如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )| A. | 60° | B. | 80° | C. | 90° | D. | 100° |
20.观察如图图形的构成规律,根据此规律,第n个图形中圆的个数是( )


| A. | n2-1 | B. | n2 | C. | n2+2n | D. | n2+1 |
 如图,在直角坐标系中,B点的坐标为(a,b),且a,b满足b=$\frac{\sqrt{{a}^{2}-4}+\sqrt{4-{a}^{2}}+8}{a+2}$
如图,在直角坐标系中,B点的坐标为(a,b),且a,b满足b=$\frac{\sqrt{{a}^{2}-4}+\sqrt{4-{a}^{2}}+8}{a+2}$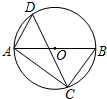 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°.
如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°.