题目内容
10.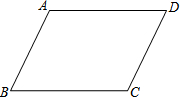 证明:两组对角分别相等的四边形是平行四边形.
证明:两组对角分别相等的四边形是平行四边形.已知:在四边形ABCD中:∠A=∠C,∠B=∠D
求证:四边形ABCD为平行四边形.
分析 由已知条件和四边形内角和定理得出∠A+∠B=180°,∠B+∠C=180°,证出AD∥BC,AB∥CD,即可得出结论.
解答 证明:∵∠A=∠C,∠B=∠D,∠A+∠C+∠B+∠D=360°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD,
∴四边形ABCD为平行四边形(两组对边分别平行的四边形是平行四边形).
点评 本题考查了平行四边形的判定方法、四边形内角和定理、平行线的判定;熟练掌握四边形内角和定理、平行线的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知反比例函数y=$\frac{4}{x}$,则当-4<x<-1时,y的取值范围是( )
| A. | 1<y<4 | B. | -4<y<-2 | C. | -4<y<-1 | D. | 2<y<4 |
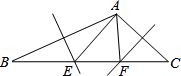 如图,△ABC中,∠BAC=110°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为40°.
如图,△ABC中,∠BAC=110°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为40°.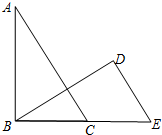 已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.
已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.