题目内容
19.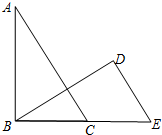 已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.
已知如图:△ABC和△BED中,∠ABC=∠BDE=90°,AC∥DE,BC=DE;求证:AC=BE.
分析 根据AC∥DE,可知∠ACB=∠E,又∠ABC=∠BDE=90°,BC=DE,证明△ABC≌△BDE即可.
解答 证明:∵AC∥DE,
∴∠ACB=∠E,
在△ABC和△BDE中,
$\left\{\begin{array}{l}{∠ACB=∠E}\\{BC=DE}\\{∠ABC=∠BDE=90°}\end{array}\right.$,
∴△ABC≌△BDE(ASA),
∴AC=BE.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
10.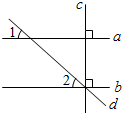 如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=60°,则∠2等于( )
如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=60°,则∠2等于( )
 如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=60°,则∠2等于( )
如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=60°,则∠2等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
6.小丰妈妈买了一部29英寸(74cm)电视机,下列对29英寸的说法中正确的是( )
| A. | 指的是屏幕的长度 | B. | 指的是屏幕的宽度 | ||
| C. | 指的是屏幕的周长 | D. | 是屏幕对角线的长度 |
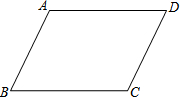 证明:两组对角分别相等的四边形是平行四边形.
证明:两组对角分别相等的四边形是平行四边形. 如图,AB是⊙O的直径,C是半圆上的一个三等分点,D是$\widehat{AC}$的中点,P是直径AB上一点,⊙O是半径为1,则PC+PD的最小值是$\sqrt{2}$.
如图,AB是⊙O的直径,C是半圆上的一个三等分点,D是$\widehat{AC}$的中点,P是直径AB上一点,⊙O是半径为1,则PC+PD的最小值是$\sqrt{2}$.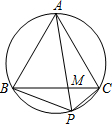 如图,点P为等边△ABC外接圆,劣弧为BC上的一点.
如图,点P为等边△ABC外接圆,劣弧为BC上的一点.