题目内容
12. 如图,在矩形ABCD中,点E是边BC上一点,AE=AD,DF⊥AE,垂足为F,线段DF与图中的哪些线段相等?证明你的结论.
如图,在矩形ABCD中,点E是边BC上一点,AE=AD,DF⊥AE,垂足为F,线段DF与图中的哪些线段相等?证明你的结论.
分析 AE=AD,且分别是△ABE、△DFA的两条边,DF是△DFA的边,可试证两三角形是否全等,则找到和DF相等的边.
解答 解:AB.
理由如下:
在△EAB与△ADF中,
$\left\{\begin{array}{l}{AE=AD}\\{∠AEB=∠DAF}\\{∠ABE=∠DFA=90°}\end{array}\right.$,
∴△EAB≌△ADF(AAS),
∴DF=AB
点评 本题考查矩形的性质,关键是根据全等三角形的判定和性质解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列奥运会徽中,中心对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
10.已知二元一次方程5x-6y=20,当y<0时,x的取值范围是( )
| A. | x>4 | B. | x<4 | C. | x>-4 | D. | x<-4 |

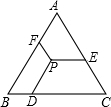 如图,P是等边三角形ABC内任一点,过点P作PD∥AB,PE∥BC,PF∥AC,分别交BC、AC、AB于点D、E、F.求证:PD+PE+PF=BC.
如图,P是等边三角形ABC内任一点,过点P作PD∥AB,PE∥BC,PF∥AC,分别交BC、AC、AB于点D、E、F.求证:PD+PE+PF=BC. 如图,已知AB、CD是⊙O的弦,AB⊥CD,垂足为点E,AB被CD分成3厘米、14厘米两段(AE<EB),求点O到CD的距离.
如图,已知AB、CD是⊙O的弦,AB⊥CD,垂足为点E,AB被CD分成3厘米、14厘米两段(AE<EB),求点O到CD的距离.