题目内容
20.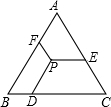 如图,P是等边三角形ABC内任一点,过点P作PD∥AB,PE∥BC,PF∥AC,分别交BC、AC、AB于点D、E、F.求证:PD+PE+PF=BC.
如图,P是等边三角形ABC内任一点,过点P作PD∥AB,PE∥BC,PF∥AC,分别交BC、AC、AB于点D、E、F.求证:PD+PE+PF=BC.
分析 因为要求证明PD+PE+PF=AB,而PD、PE、PF并不在同一直线上,因此和AB无法进行比较,必须把三者转移到AB上,方可解答.
解答 证明:延长EP交AB于点G,延长DP交AC与点H,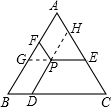
∵PD∥AB,PE∥BC,PF∥AC,
∴四边形AFPH、四边形PDBG均为平行四边形,
∴PD=BG,PH=AF.
又∵△ABC为等边三角形,
∴△FGP和△HPE也是等边三角形,
∴PE=PH=AF,PF=GF,
∴PE+PD+PF=AF+BG+FG=AB=BC.
点评 本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
10.计算:|3-π|=( )
| A. | 3 | B. | 3-π | C. | 0.14 | D. | π-3 |
11. 如图,△ABC的内切圆O与各边分别相切于D,E,F三点,则点O是△DEF的( )
如图,△ABC的内切圆O与各边分别相切于D,E,F三点,则点O是△DEF的( )
 如图,△ABC的内切圆O与各边分别相切于D,E,F三点,则点O是△DEF的( )
如图,△ABC的内切圆O与各边分别相切于D,E,F三点,则点O是△DEF的( )| A. | 三条中线的交点 | B. | 三条高的交点 | ||
| C. | 三条角平分线的交点 | D. | 三条边的垂直平分线的交点 |
8.在平行四边形ABCD中,∠B=30°,AB=12cm,AD=14cm,则平行四边形ABCD的面积为( )
| A. | 21cm2 | B. | 42cm2 | C. | 168cm2 | D. | 84cm2 |
 如图,在矩形ABCD中,点E是边BC上一点,AE=AD,DF⊥AE,垂足为F,线段DF与图中的哪些线段相等?证明你的结论.
如图,在矩形ABCD中,点E是边BC上一点,AE=AD,DF⊥AE,垂足为F,线段DF与图中的哪些线段相等?证明你的结论.