题目内容
16．
如图，∠ABC=90°，∠CBD=30°，BP平分∠ABC，求∠DBP的度数．
分析 先由角平分线的定义可求得∠CBP=45°，然后根据∠DBP=∠CBP-∠CBD进行求解即可．
解答 解：∵BP平分∠ABC，
∴∠CBO=$\frac{1}{2}∠CBA$=$\frac{1}{2}×90°$=45°．
∠DBP=∠CBP-∠CBD=45°-30°=15°．
点评 本题主要考查的是角平分线的定义，掌握角平分线的定义是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．一元二次方程4x2-x=1的解是（ ）
| A． | x=0 | B． | x1=0，x2=4 | ||
| C． | x1=0，x2=$\frac{1}{4}$ | D． | x1=$\frac{1+\sqrt{17}}{8}$，x2=$\frac{1-\sqrt{17}}{8}$ |
7．在同一直角坐标系中，一次函数y=2x+1与反比例函数y=$\frac{k}{x}$的图象没有交点，则k的取值范围是（ ）
| A． | k＞0 | B． | k＜0 | C． | k$＞-\frac{1}{8}$ | D． | k$＜-\frac{1}{8}$ |
4．下列方程一定是一元二次方程的是（ ）
| A． | 2x2-1=3x | B． | 2x2-y=1 | C． | ax2+bx+c=0 | D． | 2x2+$\frac{1}{x}$=1 |
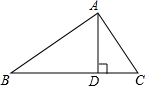如图所示，在△ABC中，作BC边上的高AD，则△ABC的面积S=$\frac{1}{2}$BC•AD，而在Rt△ABD中，sinB=$\frac{AD}{AB}$，所以AD=AB•sinB．因此，△ABC的面积S=$\frac{1}{2}AB•BC•sinB$．
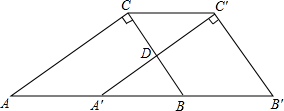已知：如图，在Rt△ABC中．∠ACB=Rt∠，AC=4，BC=3．将△ABC沿AB方向平移至△A′B′C，使A′C′经过BC的中点D．
如图，C为线段AB上一点，D为线段BC的中点，AB=10cm，BC=acm，（5＜a＜10），求线段AC的长（用含a的式子表示）．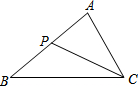
如图，P是△ABC的边AB上一点，请添加一个条件使得△ABC与△ACP相似，则你添加的条件可以是∠B=∠ACP．（只需添加一个符合的条件即可）