题目内容
1.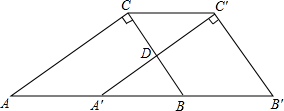 已知:如图,在Rt△ABC中.∠ACB=Rt∠,AC=4,BC=3.将△ABC沿AB方向平移至△A′B′C,使A′C′经过BC的中点D.
已知:如图,在Rt△ABC中.∠ACB=Rt∠,AC=4,BC=3.将△ABC沿AB方向平移至△A′B′C,使A′C′经过BC的中点D.(1)求证:AA′=A′B=BB′.
(2)求梯形AB′C′C的面积.
分析 (1)根据平移的性质,可得AA′,BB′,CC′的关系,根据全等三角形的判定与性质,可得A′B与CC′DEGUANXI,
(2)根据三角形的面积,可得梯形的高,根据梯形的面积公式,可得答案.
解答 (1)证明:∵△ABC沿AB方向平移至△A′B′C,
∴AA′=BB′=CC′.
∴CC′∥AB′,
∴∠CC′D=BA′D,∠DCC′=∠A′BD.
在△A′BD和△C′CD中,
$\left\{\begin{array}{l}{∠BA′D=∠CC′D}\\{∠A′BD=∠C′CD}\\{A′D=C′D}\end{array}\right.$,
∴△A′BD≌△C′CD (AAS),
∴A′B=C′C,
∴AA′=A′B=BB′.
(2)解:如图: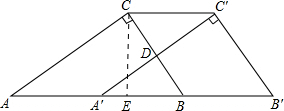 ,
,
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,CC′=AA′=A′B=$\frac{5}{2}$,
由S△ABC=$\frac{1}{2}$AB•CB=$\frac{1}{2}$AB•CE.
CE=$\frac{3×4}{5}$=$\frac{12}{5}$,
S梯形AB′C′C=$\frac{1}{2}$(CC′+AB′)•CE=$\frac{1}{2}$($\frac{5}{2}$+5+$\frac{5}{2}$)×$\frac{12}{5}$=12.
点评 本题考查了平移的性质,利用了平移的性质,全等三角形的判定与性质.

练习册系列答案
相关题目
11.下面计算中正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | -1-1=1 |
9.在Rt△ABC中,∠C=90°,若sinA=$\frac{\sqrt{3}}{2}$,则sin$\frac{A}{2}$的值是( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
10.在Rt△ABC中,∠ACB=90°,AC=24cm,AB=26cm,则其直角边BC的长为( )
| A. | 6cm | B. | 100cm | C. | 15cm | D. | 10cm |
 如图,∠ABC=90°,∠CBD=30°,BP平分∠ABC,求∠DBP的度数.
如图,∠ABC=90°,∠CBD=30°,BP平分∠ABC,求∠DBP的度数.
 已知:如图,AB=CD,AB∥CD,DE⊥AC,BF⊥AC,E、F是垂足,AF=5,求CE的长.
已知:如图,AB=CD,AB∥CD,DE⊥AC,BF⊥AC,E、F是垂足,AF=5,求CE的长. C、D两点把线段AB分成2:3:4三部分,M是AB的中点,CD=8.
C、D两点把线段AB分成2:3:4三部分,M是AB的中点,CD=8.